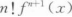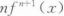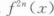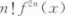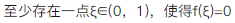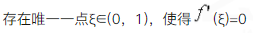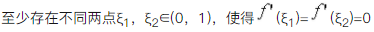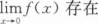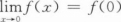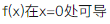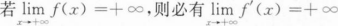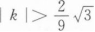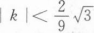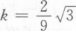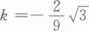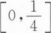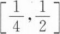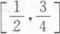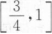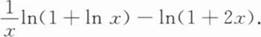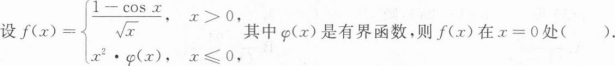
设f(x)可导且f`(x0)=1/2，则当△x→0时，f(x)在x0处的微分dy是△x的（） 无穷小．
设f(x)有一阶连续导数，F(x)=f(x)(1+|sinx|)，则f(0)=0是F(x)在x=0处可导的（）．
已知y=x3+ax2+bx+c在x=-2处取得极值，且与直线y=-3x+3相切于点(1，0)，则（）．
设f(x)在[0，+∞)上二阶可导，f(0)=0，f``(x)<0，当0<a<x<b时，有（）．
设f(x)在[0，1]上有二阶导数，且f(0)=f(1)，f``(x)≠0，则下列选项正确的是（）．
设f(x)在x=0的某邻域内有定义，则F(x)=f(x)|sinx|在x=0处可导的充要条件是（）．
设f(x)在(-∞，+∞)内可导，则下列命题正确的是（）．
设f(x)在[0，+∞)上二阶可导，f(0)=0，f`(0)<0，f``(x)≥M>0，则方程f(x)=0在(0，+∞)内不同实根的个数为（）．
设函数f1(X)，f2(X)有二阶连续导数，且f1``(x)>0，f2``(x)>0，若曲线y=f1(x)与y=f2(x)在点(x0，y0)处有公切线y=g(x)，且在该点处曲线y=f1(x)的曲率半径小于y=f2(x)的曲率半径，则在点x0的某邻域内有（）．
ln(1+lnx)-ln(1+2x)．
ln(1+lnx)-2ln(1+2x)．
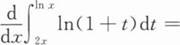
根据题意回答问题。
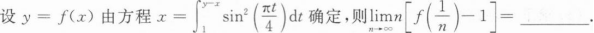
根据题意回答问题。
则f`(0)=_______．
根据题意回答问题。
当x→0时．x-sinxcosx与axb为等价无穷小，则a=_______，b=_______．
根据题意回答问题。
根据题意回答问题。
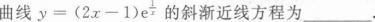
根据题意回答问题。
根据题意回答问题。
设连续函数y=f(x)在点(1，0)处满足△y=△x+o(△z)，则极限
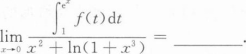
根据题意回答问题。
根据题意回答问题。
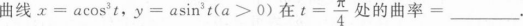
根据题意回答问题。
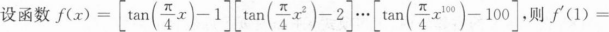
根据题意回答问题。
设f(x)=3x2+kx-3，若对任意x∈(0，+∞)，都有f(x)≥20，则k至少为_______．
根据题意回答问题。
根据题意回答问题。
已知f(x)在(-∞，+∞)内可导，且
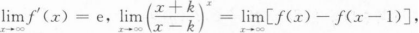
则k=_______．
根据题意回答问题。
设f(x)在x=x0处可导，且f(x0)≠0，则
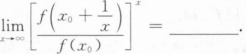
根据题意回答问题。
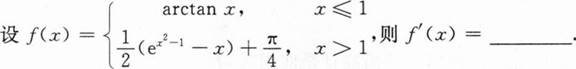
根据题意回答问题。
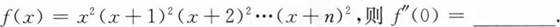
根据题意回答问题。
根据题意回答问题。
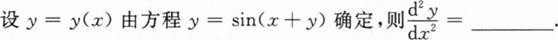
根据题意回答问题。
根据题意回答问题。
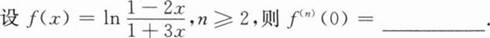
根据题意回答问题。
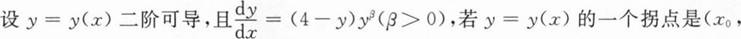
3)，则β=_____．
根据题意回答问题。
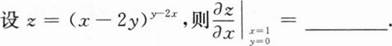
根据题意回答问题。
f(x)=ln(2+x-3x2)在x=0处的泰勒展开式为______．
根据题意回答问题。
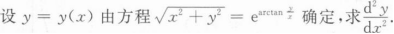
根据题意回答问题。
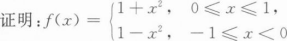
满足拉格朗日中值定理，并求满足定理的ξ 的值．
根据题意回答问题。
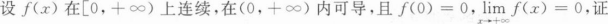
明：至少存在一点ξ∈(0，+∞)，使得f`(ξ)=0．
根据题意回答问题。
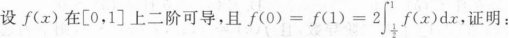
至少存在一点ξ(0，1)，使得f``(ξ)=0；
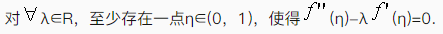
设f(x)在[a，b]上连续，在(a，b)内可导，0<a<b，证明：存在ξ，η∈(a，b)，使得2ηf`(ξ)=(b+a)f`(η).
根据题意回答问题。
根据题意回答问题。
对数曲线y=lnx上哪一点的曲率半径最小?求出该点的曲率半径．
根据题意回答问题。
证明：方程2x-x2-1=0有且仅有三个不同实根．
根据题意回答问题。
已知f(x)是周期为5的连续函数，f(x)在x=1的某邻域内满足 f(1+sinx)-3f(1-sinx)=8x+a(x)， 其中a(x)是当x→0时比x高阶的无穷小，且f(x)在x=1处可导，求曲线y=f(x)在点(6，f(6))处的切线方程．
根据题意回答问题。
在x=0的右邻域内，用多项式e+ax+bx2近似表示函数，
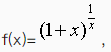
使其误差是比x2高阶的无穷小(x→0+)，求a，b的值．
根据题意回答问题。
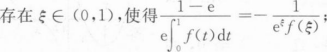
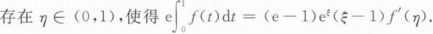
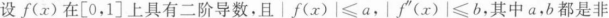
负常数，c是(0，1)内任一点．
写出f(x)在x=c处带拉格朗日余项的一阶泰勒公式；
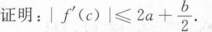
已知f(x)可导，证明：曲线y=f(x)(f(x)>0)与曲线y=f(x)sinx在交点处相切．
根据题意回答问题。
设R=R(x)是抛物线y=
上任一点M(x，y)(x≥1)处的曲率半径，s=s(x)
根据题意回答问题。
根据题意回答问题。
