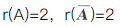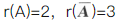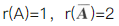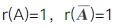设A是n阶矩阵,对方程组(Ⅰ)Ax=0和(Ⅱ)ATAx=0,必有().
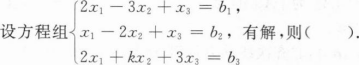
设A是m×n矩阵,则非齐次线性方程组Ax=b有无穷多解的充分必要条件是().
设三个不同平面的方程为ai1x+ai2y+ai3z=bi(i=1,2,3)相交于一条直线,三个平面方程组成方程组的系数矩阵和增广矩阵分别记为A和
,则().
设AT=(α1,α2,…,αn-1)是n×(n-1)矩阵,r(AT)=n-1,β1,β2是与α1,α2,…,αn-1都正交的两个不同的n维列向量,k是任意常数,则方程组Ax=0的通解为().
已知A=[α1,α2,α3,α4]是4阶矩阵,η1=(3,1,-2,2)T,η2=(0,-1,2,1)T。是Ax=0的基础解系,则下列命题中正确的一共有
①α1一定可由α2,α3线性表示.②α1,α3是A列向量的极大线性无关组.③秩r(α1,α1+α2,α3-α4)=2.④α2,α4是A列向量的极大线性无关组.
设A是n阶矩阵,对于齐次线性方程组(Ⅰ)Anx=0和(Ⅱ)An+1x=0,现有四个命题
①(Ⅰ)的解必是(Ⅱ)的解;②(Ⅱ)的解必是(Ⅰ)的解;
③(Ⅰ)的解不是(Ⅱ)的解;④(Ⅱ)的解不是(Ⅰ)的解.以上命题中正确的是
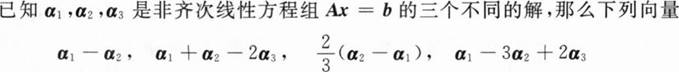
中是导出组Ax=0解的向量共有
已知α1,α2,α3是齐次方程组Ax=0的基础解系,则Ax=0的基础解系还可以是
设A=(aij)3×3为实矩阵,且Aij=aij(i,j=1,2,3),其中Aij为aij的代数余子式, a33=1,|A|=1,则方程组

根据题意回答问题。

根据题意回答问题。
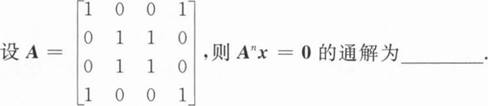
根据题意回答问题。
设A是5×4矩阵,若η1,η2是齐次方程组Ax=0的基础解系,则r(AT)=____.
根据题意回答问题。
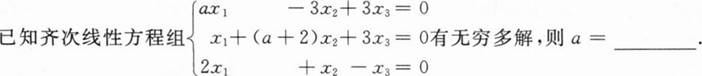
根据题意回答问题。
已知方程组
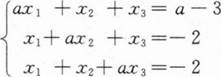
有无穷多解,则a=______.
根据题意回答问题。
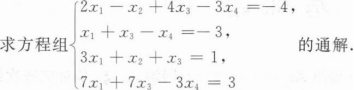
根据题意回答问题。

解?当有无穷多解时,求其通解.
根据题意回答问题。
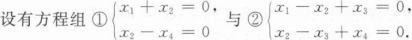
求方程组①与②的基础解系;
求方程组①与②的非零公共解.
设有方程组

求方程组①的通解;
当a,b,c为何值时,方程组①与②同解.
已知4×3矩阵A=(α1,α2,α3),非齐次线性方程组Ax=β的通解为(1,2,-1)T+ k(1,-2,3)T,k为任意常数,令B=(α1,α2,α3,β+α3),求方程组By=α1-α2的通解.
根据题意回答问题。
设A是3阶方阵,A=(aij)3×3,且aij=Aij,i,j=1,2,3,其中Aij为aij的代数余子式,a33≠0,b=(a13,a23,a33)T,求非齐次线性方程组Ax=b的解.
根据题意回答问题。
设A是5×4矩阵,r(A)=2,已知α1,α2,α3是非齐次线性方程组Ax=b的三个解向量,且α1+α2=(4,6,-8,4)T,α3=(1,2,-1,1)T,又(0,1,-3,0)T是Ax=0的解,求Ax=b的通解.
根据题意回答问题。
设A是3阶矩阵,向量β=(3,3,3)T,非齐次线性方程组Ax=β的通解为 k1(1,2,-2)T+k2(2,1,2)T+(1,1,1)T,k1,k2为任意常数.
证明:任意3维列向量口可由A的三个特征向量线性表示;
若α=(1,2,-1)T,求Aα.
已知A(1,1),B(2,2),c(a,1)为坐标平面上的点,其中a为参数,问是否存在经过点A,B,C的曲线y=k1x+k2x2+k3x3? 如果存在,求出曲线方程.
根据题意回答问题。
设方程组
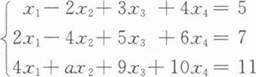
当a为何值时方程组有解?并求其通解.
求方程组满足x1=x2的所有解.