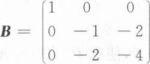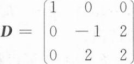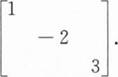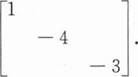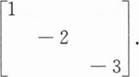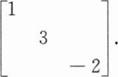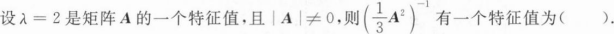
设A为3阶方阵,A的三个特征值为1,1,2,α1,α2,α3分别为对应的三个特征向量,则().
A-1~B-1,则下列结果
①AB~BA②A~B③A2~B2④AT~BT
中正确的个数为().


B的特征值是
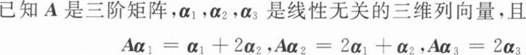
下列矩阵中,不能相似对角化的矩阵是

已知A是行阶可逆矩阵,那么与A有相同特征值的矩阵是
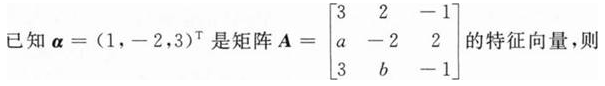
设A是n阶矩阵,下列命题中正确的是
设A是三阶矩阵,其特征值是1,3,-2,相应的特征向量依次为α1,α2,α3,若P=[α1,2α3,-α2],则P-1AP=
设A是三阶矩阵,特征值是2,2,-5.α1,α2是A关于λ=2的线性无关的特征向量,α3是A对应于λ=-5的特征向量.若
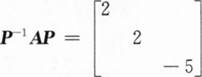
,则P不能是
已知A是三阶矩阵,r(A)=1,则λ=0
设n阶方阵B=AA*,则B的特征值为_______,特征向量为_______.
根据题意回答问题。
设方阵A满足A2+2A+E=0,则A有特征值_______.
根据题意回答问题。
设A3×3是秩为1的实对称矩阵,λ1=2是A的一个特征值,对应的特征向量为α1=(-1,1,1)T,则方程组Ax=0的基础解系为.
根据题意回答问题。
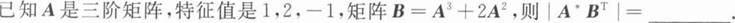
根据题意回答问题。

根据题意回答问题。
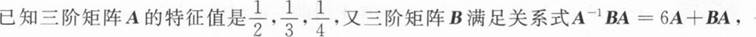
则矩阵B的特征值是____.
根据题意回答问题。

根据题意回答问题。

的逆矩阵的特征向量,那么α在矩阵A中对应的特征值是______.
根据题意回答问题。

根据题意回答问题。
已知A是三阶矩阵,且矩阵A各行元素之和均为5,则矩阵A必有特征向量_____.
根据题意回答问题。
已知A是三阶实对称矩阵,特征值是1,3,-2,其中α1=(1,2,-2)T,α2=(4,-1,a)T分别是属于特征值λ=1与λ=3的特征向量,那么矩阵A属于特征值λ=-2的特征向量是_____.
根据题意回答问题。
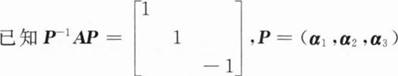
可逆,则矩阵A关于特征值λ=1的特征向量是______.
根据题意回答问题。

根据题意回答问题。

根据题意回答问题。

求A的全部特征值和特征向量;
求可逆矩阵P,使得P-1AP=A;
求正交矩阵Q,使Q-1AQ=A.
判别下列矩阵A与B是否相似.若相似,求可逆矩阵P,使得P-1AP=B.
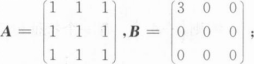
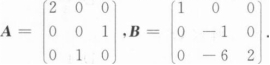

求a的值;
求可逆矩阵P,使得P-1AP为对角矩阵.

α1=(1,1,0)T,α2=(0,2,1)T.
求A的特征值与特征向量;
求可逆矩阵P,使得P-1AP=A.
设3阶实对称矩阵A的特征值为λ1=λ2=1,λ3=-1,α1=(1,1,1)T,α2=(2,2,1)T是λ1=λ2=1对应的特征向量.
求A的属于λ3=-1的特征向量;
求矩阵A.
(Ⅰ)已知A=(α1,α2,α3)是3阶可逆矩阵,B是3阶矩阵,且BA=(α1,-4α3,-α2).
(Ⅰ)求B的全部特征值;
(Ⅱ)求可逆矩阵P和对角矩阵A,使得P-1BP=A.
根据题意回答问题。

求可逆矩阵P,使得P-1AP=A;
求(2E-A2)-1.

求可逆矩阵P及对角矩阵A,使得P-1AP=A;
求r(A*).
设α,β为3维单位列向量,且αTβ=0,记A=αβT+βαT.
证明:A相似于对角矩阵;
若存在3维列向量γ≠0,使得Aγ=0,记P=(γ,2(α+β),β-α),求P-1AP.
设A,B均是n阶矩阵.
证明:AB与BA有相同的特征值;
若AB=BA,且A有n个不同的特征值,证明:B相似于对角矩阵.

得P-1AP=B.
根据题意回答问题。

求a的值.
求正交变换x=Qy化二次型为标准形,并写出所用坐标变换.
若A+kE是正定矩阵,求k.