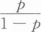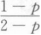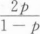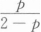设二维随机变量(X,Y)的分布函数为F(x,y),则P{X>x0,Y>y0)=().
设随机变量X与Y独立同分布,均服从P{X=k}=p(1-p)k-1,k=1,2,…,0<p<1,则P{X=Y}=().
设A,B,C为三个随机事件,且A与C相互独立,B与C相互独立,则A-B与C相互独立的充分必要条件是
设相互独立的随机变量x和y均服从P(1)分布,则P{X=1|X+Y=2)的值为
已知(X,Y)服从二维正态分布,EX=EY=μ,DX=DY=σ2,X与Y的相关系数ρ≠0,则X与Y
设随机变量X与Y相互独立,X服从参数为A的指数分布,Y的分布律为
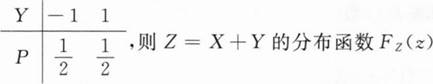
已知随机变量X与Y相互独立且都服从正态分布N(μ,1/2),如果P{x+y≤1}=1/2,则μ等于
设随机变量X和Y相互独立,均服从分布B(1,1/2),则成立
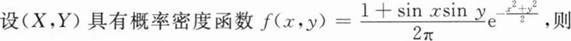
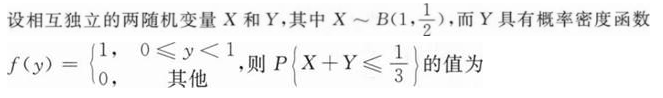
设相互独立的两随机变量x和y均服从分布B(1,1/3),则P{X≤2Y}=
设随机变量X,Y独立同分布,且X的分布函数为F(x),则Z=min(X,Y)的分布函数为
设相互独立的两随机变量X,Y均服从[0,3]上的均匀分布,则P{1<max(X,Y)≤2)的值为
设相互独立的两随机变量X和Y分别服从E(λ),λ>0,和E(λ+2)分布,则P{min(X,Y)>1}的值为
假设总体X服从正态分布N(μ,σ2),X1,…,Xn是取自总体X的简单随机样本(n>1),
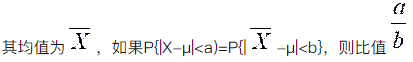
设二维随机变量(X,Y)的分布律为
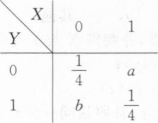
且事件{X=0)与{X+Y=1}相互独立,则a______,b______.
根据题意回答问题。
设随机变量X,Y均服从区间为[0,4]的均匀分布,P{max{X,Y}≤3)=9/16,则P{min{X,Y)>3)=______.
根据题意回答问题。
已知随机变量X与y都服从正态分布N(μ,σ2),如果P{max(x,y)>μ}=a(0<a<1),则P{min(X,Y)≤μ}=_____.
根据题意回答问题。

1}=______.
根据题意回答问题。
设随机变量X1和X2相互独立,已知X1~B(1,3/4),X2的分布函数为F(x),则随机变量Y=X1十X2的分布函数FY(y)=______.
根据题意回答问题。
设随机变量X与Y相互独立,且均服从正态分布N(μ,σ2),则P{max(X,y)>μ}-P{min(X,Y)<μ}=______.
根据题意回答问题。
设相互独立两个随机变量X和Y均服从标准正态分布,则随机变量X-Y的概率密度函数的最大值等于______.
根据题意回答问题。
设二维随机变量(X,Y)的分布函数为φ(2x+1)φ(2y-1),其中φ(x)为标准正态分布函数,则(X,Y)服从正态分布N(_____).
根据题意回答问题。
设随机变量X和Y相互独立,且X服从标准正态分布,其分布函数为φ(x),Y的概率分布为P{Y=-1}-P{Y=1}=1/2,则随机变量Z=XY的分布函数F(x)=______.
根据题意回答问题。
设随机变量X和Y相互独立,X在区间(0,1)内服从均匀分布,Y的概率密度为
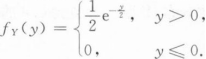
求(X,Y)的联合概率密度;
设X和Y满足关于k的二次方程,k2+2Xk+Y=0,求k有实根的概率.
设X与Y相互独立,x服从参数为1/2的指数分布,Y服从参数为1/3的指数分布,求Z=X+Y的概率密度.
根据题意回答问题。
设(X,Y)服从区域G={(x,y)|0≤x≤2,0≤y≤1)上的均匀分布,求Z=XY的分布函数与概率密度.
根据题意回答问题。
在区间[0,1]上随机地掷两点,求这两点间距离的概率密度.
根据题意回答问题。
设二维随机变量(X,Y)在D={(x,y)|0≤x≤2,0≤y≤1)上服从均匀分布, 令
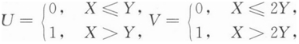
,求(U,V)的联合分布律,并判别U与V是否相互独立.
根据题意回答问题。
设二维随机变量(X,Y)服从D={(x,y)|y≥0,x2+y2≤1}上的均匀分布,令
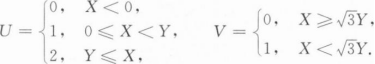
求(U,V)的联合概率分布;
求P{UV≠0).

求k的值及P{X1<0,X2<1);
求(Y1,Y2)的概率分布.
设二维随机变量(X,Y)的概率密度为

证明:Y服从参数为λ的指数分布;
问X与Y是否相互独立?并说明理由.
设随机变量x和y相互独立,X~N(0,1),Y~U[0,1],Z=X+Y,求Z的概率密度函数fZ(z).
根据题意回答问题。
设二维随机变量(X,Y)的概率密度为
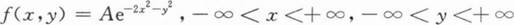
求常数A;
求条件概率密度fY|X(y|x).
二维随机变量(X,Y)的概率密度为f(x,y),-∞<x<+∞,-∞<Y<+∞. 已知X的密度
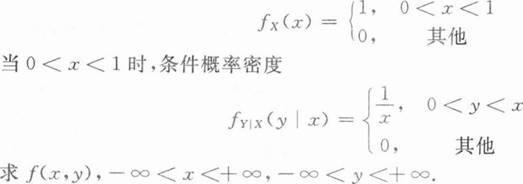
根据题意回答问题。