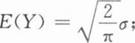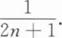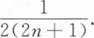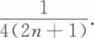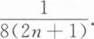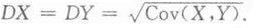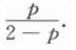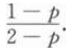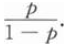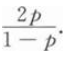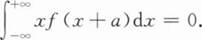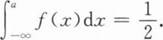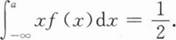设随机变量X服从参数为2的指数分布,则Y=2X+e-2x的期望EY=().
设随机变量x,有EX=μ,DX=σ2(μ,σ为常数),则对任意常数C,下列选项正确的是().
设X~N(0,1),Y~N(1,4),且ρXY=1,则().
设对任意两个随机变量X与y,有E(XY)=EX·EY,则().
设随机变量X与Y相关,相关系数为ρXY,Z=aX+b(a,b为常数),则ρYZ=ρXY的充分必要条件为().
现有10张奖券,其中8张2元,2张5元,今从中一次取三张,则得奖金X的数学期望EX为
设随机变量x~B(1.1/2),y~B(1,1/2).已知x与y的相关系数ρ=1,则P{X=0,Y=1}的值必为
甲、乙两袋中各装有n个红球和n个白球(n>1),先从甲袋中任取一球,观察颜色后放入乙袋中,再从乙袋中任取一球,令X,Y分别表示从甲袋和从乙袋中取到的红球个数,则Cov(X,Y)为
设随机变量X与Y的方差均为正,则X与Y的相关系数ρ=1的充要条件为

设随机变量X的二阶矩存在,则
设随机变量X的期望、方差都存在,则对任意常数c,有
设随机变量X的概率密度函数为f(x),则其数学期望E(x)=a,如果成立
设随机变量X服从标准正态分布N(0,1),则E[(x-2)2e2x]=
已知随机变量X与Y有相同的不为零的方差,则X与Y相关系数等于1的充分必要条件是
设随机变量X的EX=μ,DX=σ2(σ>0为常数),则对任意常数c必有
假设随机变量X与y相互独立具有非零的方差,DX≠DY,则
相互独立同分布的两个随机变量X1和X2,已知
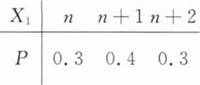
则D(X1+X2)=
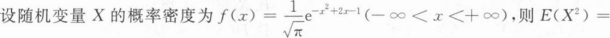
根据题意回答问题。
设随机变量X的概率分布为P{X=k}=
(k=0,1,2,…),则E(X2)=________.
根据题意回答问题。
设随机变量X1,X2,…,Xn独立同分布,且有相同的概率密度,则概率P{Xn>min{X1,X2,…,Xn-1}}=________.
根据题意回答问题。
设15000件产品中有1000件次品,从中任取150件进行检测,则检测到次品数X的期望EX=________.
根据题意回答问题。
设(X,Y)~N(1,1,2,2;0),U=X+2Y,V=X-2y,则ρUV=________.
根据题意回答问题。
已知随机变量X在(1,2)上服从均匀分布,在X=x(1<x<2)的条件下Y服从参数为x的指数分布,则E(XY)=_____.
根据题意回答问题。
设随机变量x~B(n,p),且E(x)=3.2,D(X)=0.64,则P{X≠0)=_____.
根据题意回答问题。
设X1,X2,…,Xn来自总体x~N(μ,σ2)的简单随机样本,记样本方差S2,则D(S2)=____.
根据题意回答问题。
已知随机变量X1与X2相互独立且分别服从参数为λ1,λ2的泊松分布,已知P{X1+X2>0}=1-e-1,则E(X1+X2)2=.
根据题意回答问题。
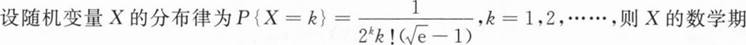
望E(X)=______.
根据题意回答问题。

根据题意回答问题。
设随机变量x和y均服从B(1,1/2),且D(X+Y)=1,则X与Y的相关系数ρ=____.
根据题意回答问题。
设随机变量X服从分布E(1),记Y=min{|X|,1},则Y的数学期望E(Y)=
根据题意回答问题。

根据题意回答问题。
设随机变量X服从参数为λ的泊松分布,且已知E[(X-1)(X-2)]=1,则λ=
根据题意回答问题。

根据题意回答问题。
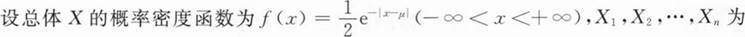
总体X的简单随机样本,其样本方差为S2,则E(S2)=____.
根据题意回答问题。
设随机变量X与Y相互独立,
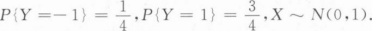
求Z=XY的概率密度;
求Coy(Z,X).
设二维随机变量(X,Y)服从区域D={(x,y)|0≤x≤2,0≤y≤2}上的均匀分布.
求Z=X+Y的概率密度;
)求E(Z2).
在区间(0,1)内随机取n个数X1,X2,…,Xn.
求最大数与最小数之间距离d的数学期望;
若用Y表示n个数中大于2/3的个数,求EY和DY.
设随机试验E有三种两两不相容的结果A1,A2,A3,且三种结果发生的概率均为1/3,将试验E独立重复做2次,X表示2次试验中结果A1发生的次数,Y表示2次试验中结果A2发生的次数.
求(X,Y)的联合分布律;
求ρXY.
设X1,X2,…,Xn相互独立同分布,其相同的概率密度为

根据题意回答问题。
设X1与X2相互独立,Xi~B(i,p)(i=1,2,0<p<1),令
求Cov(Y1,Y2);
确定p的值,使Cov(Y1,Y2)取值最小.
设随机变量X1与X2相互独立,且X1~B(1,p),X2~B(2,p),其中0<p<1,令Y1=2X1+X2,Y2=X1-X2.
求相关系数ρY1Y2;
问Y1与Y2是否相互独立?并说明理由.
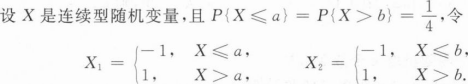
求(X1,X2)的联合分布及边缘分布;
求Cov(X1,X2),D(X1-X2).
设随机变量X和Y独立同分布,已知X~N(μ,σ2),求Z=min(X,Y)的数学期望E(Z).
根据题意回答问题。

求Cov(X,Z).
根据题意回答问题。

试证: