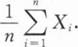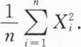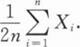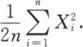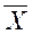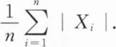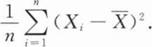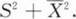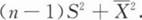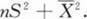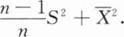第7节 参数估计
单选题: 3题简答题: 13题总题量: 16题
1
[单选题]

收藏
纠错
解析
2
[单选题]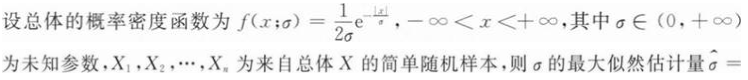
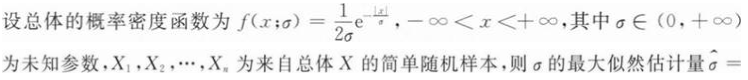
收藏
纠错
解析
3
[单选题]

收藏
纠错
解析
4
[简答题]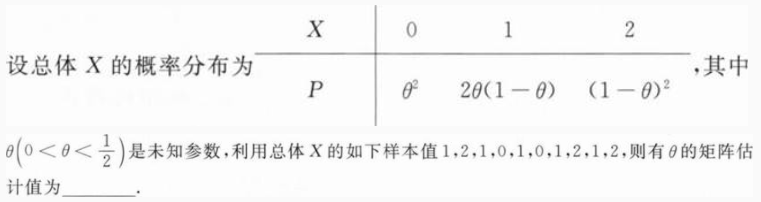

收藏
纠错
解析
问题:
1、
未作答根据题意回答问题。
5
[简答题]
设随机变量x在区间[0,θ]上服从均匀分布,X1,X2,…,Xn是来自总体X的简单随机样本,则θ的最大似然估计量
收藏
纠错
解析
问题:
1、
未作答根据题意回答问题。
6
[简答题]

收藏
纠错
解析
问题:
1、
未作答根据题意回答问题。
7
[简答题]

收藏
纠错
解析
问题:
1、
未作答根据题意回答问题。
8
[简答题]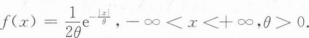
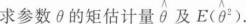
设X1,X2,…,Xn是来自总体X的简单随机样本,X的概率密度为
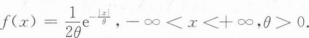
收藏
纠错
解析
问题:
1、
未作答根据题意回答问题。
9
[简答题]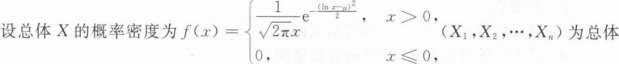
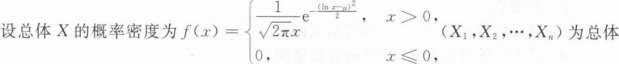
X的简单随机样本.
收藏
纠错
解析
问题:
1、
未作答
2、
未作答
10
[简答题]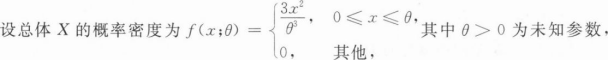
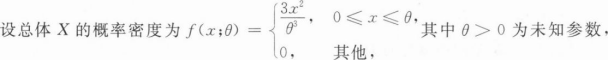
收藏
纠错
解析
问题:
1、
未作答根据题意回答问题。
11
[简答题]
设总体X服从参数为λ的泊松分布,(X1,X2,…,Xn)是总体X的样本,
S2是样本方差.
收藏
纠错
解析
问题:
1、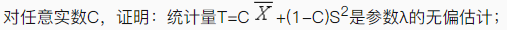
未作答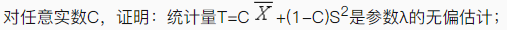
2、
未作答求概率P{X≥1}的最大似然估计量.
12
[简答题]
设总体X~N(μ,σ2),μ,σ2为未知参数,(x1,x2,…,xn)为总体X的简单随机样本值,求μ,σ2的最大似然估计量.
收藏
纠错
解析
问题:
1、
未作答根据题意回答问题。
13
[简答题]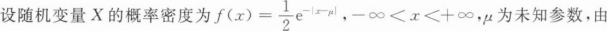
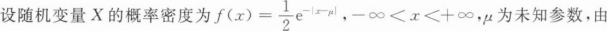
样本值:1028,968,1007,求μ的矩估计值和最大似然估计值.
收藏
纠错
解析
问题:
1、
未作答根据题意回答问题。
14
[简答题]
设0.50,1.25,0.80,2.00为来自总体X的简单随机样本值,Y=lnX服从正态分布N(μ,1).

收藏
纠错
解析
问题:
1、
未作答求EX;
2、
未作答求μ的置信度为0.95的置信区间;
3、
未作答求EX的置信度为0.95的置信区间.
15
[简答题]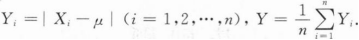
设相互独立的随机变量X1,X2,…,Xn均服从N(μ,σ2),
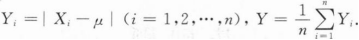
(Ⅰ)(Ⅱ) (Ⅲ)
收藏
纠错
解析
问题:
1、
未作答求Y1的概率密度;
2、
未作答利用一阶矩求σ的矩估计量;
3、
未作答求EY和DY.
16
[简答题]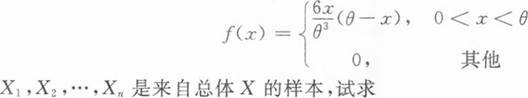
设总体X的概率密度为
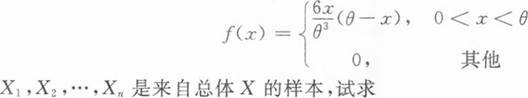
收藏
纠错
解析
问题:
1、
未作答
2、
未作答