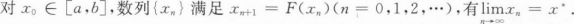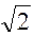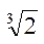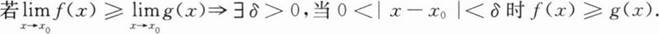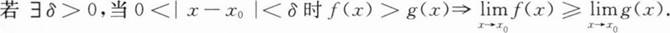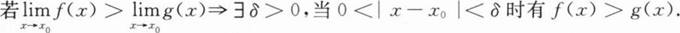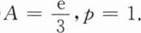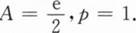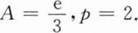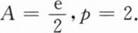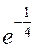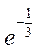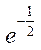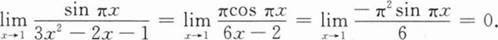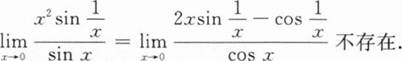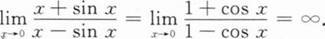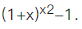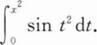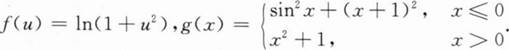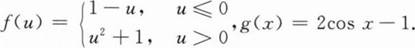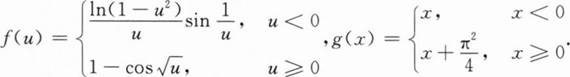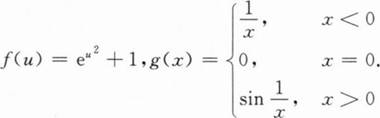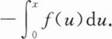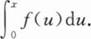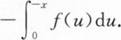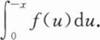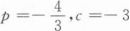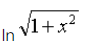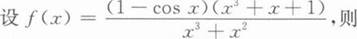
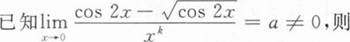
下列命题

其中正确的命题个数为
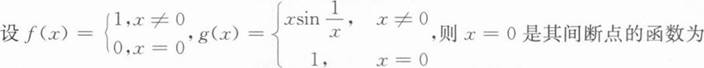
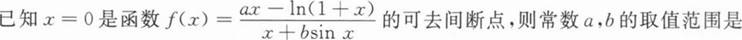
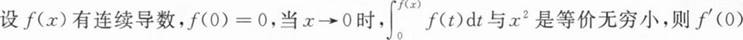
等于
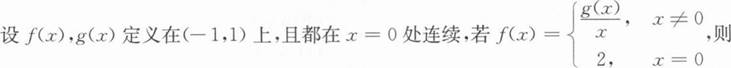
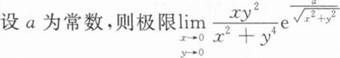
设有下列命题

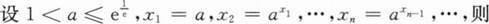
下列命题中正确的是
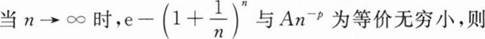
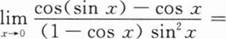
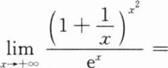
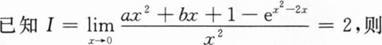
下列各题计算过程中正确无误的是
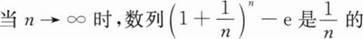
当x→0时下列无穷小中阶数最高的是
设x→a时f(x)与g(x)分别是x-a的n阶与m阶无穷小,则下列命题

以下函数f(g(x))以x=0为第二类间断点的是


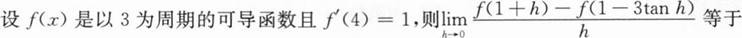
设函数g(x)在x=a点处连续,f(x)=|x-a|g(x)在x=a点处可导,则g(a)满足
设f(x)在点x=a处可导,则函数|f(x)|在点x=a处不可导的充分必要条件是
设f(x)对一切x∈(-∞,+∞)满足方程(x-1)f``(x)+2(x-1)[f`(x)]3=1-e1-x,且,(x)在x=a(a≠1)处f`(a)=0,则x=a
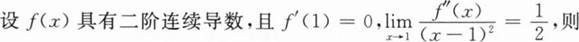
设f(x)=ax3-6ax2+b在区间[-1,2]上的最大值是3,最小值是-29,且a>0,则
以下四个命题中,正确的是
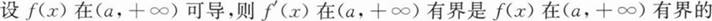
函数y=f(x)在(-∞,+∞)内连续,其二阶导函数的图形如图所示,则y=f(x)的拐点的个数是
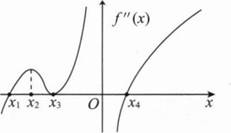
设f(x)在(1-δ,1+δ)内存在导数,f`(x)单调减少,且f(1)=f`(1)=1,则
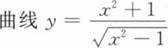
考察下列叙述:
①设f2(x)在x=x0连续,则f(x)在x=x0连续.
②设f(x)在x=x0连续,则|f(x)|在x=x0连续.
③设|f(x)|在[a,b]可积,则f(x)在[a,b]可积.
④设f(x)在[a,b]有界,只有有限个间断点,则|f(x)|在[a,b]可积,即在[a,b]存在定积分.我们可知
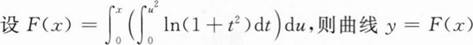
下列叙述错误的是
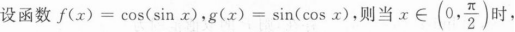
设当x→0时,(x-sinx)tanx是比ln(1+xn)高阶的无穷小,而ln(1+xn)是比x2高阶的无穷小,则n=().
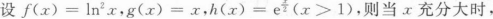
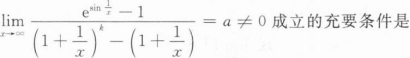
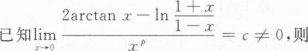
设y=y(x)是方程y"+2y'+y=e3x。的解,且满足y(0)=y'(0)=0,则当x→0时,与y(x)为等价无穷小的是().
设{xn)与(yn)为两个数列,则下列说法正确的是().
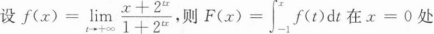
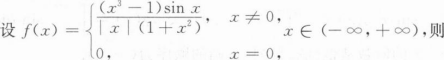
根据题意回答问题。

根据题意回答问题。
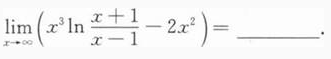
根据题意回答问题。
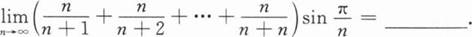
根据题意回答问题。
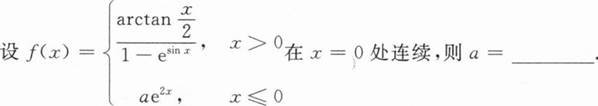
根据题意回答问题。
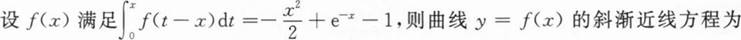
根据题意回答问题。
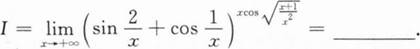
根据题意回答问题。
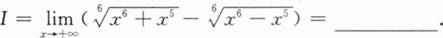
根据题意回答问题。
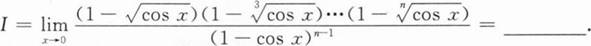
根据题意回答问题。
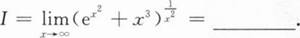
根据题意回答问题。
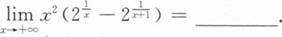
根据题意回答问题。
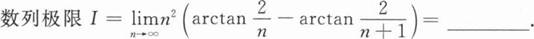
根据题意回答问题。
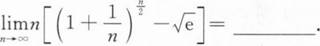
根据题意回答问题。
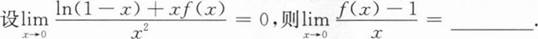
根据题意回答问题。

根据题意回答问题。
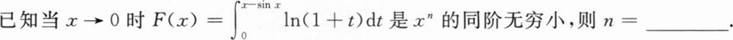
根据题意回答问题。
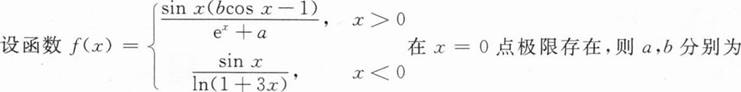
根据题意回答问题。
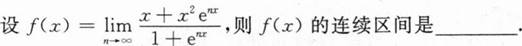
根据题意回答问题。
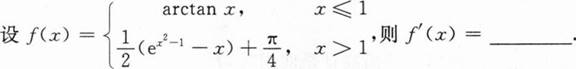
根据题意回答问题。

根据题意回答问题。

根据题意回答问题。
根据题意回答问题。
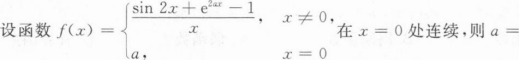
根据题意回答问题。
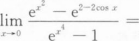
根据题意回答问题。
当x→0时,f(x)=3x-4sinx+sinxcosx是关于x的_______阶无穷小.
根据题意回答问题。
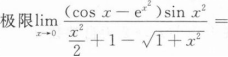
根据题意回答问题。
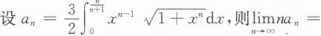
根据题意回答问题。
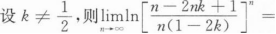
根据题意回答问题。
已知连续函数y=f(x)关于点(a,0)(a≠0)对称,则对常数c,I=
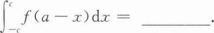
根据题意回答问题。
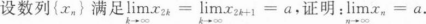
根据题意回答问题。
根据题意回答问题。
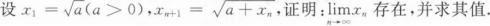
根据题意回答问题。
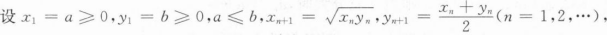
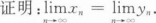
根据题意回答问题。
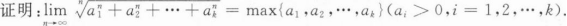
根据题意回答问题。
(Ⅰ)
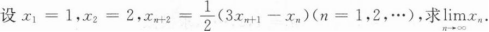
(II)
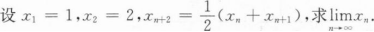
根据题意回答问题。
设fn(x)=1-(1-cosx)n(n=1,2,…).
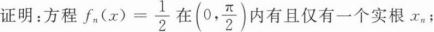

(Ⅰ)证明:方程x=1+2lnx在(e,+∞)内有唯一实根ξ;
(Ⅱ)
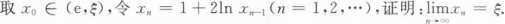
根据题意回答问题。
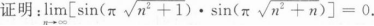
根据题意回答问题。
求下列极限: (Ⅰ)
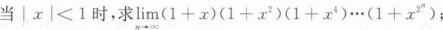
(Ⅱ)
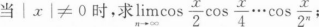
(Ⅲ)
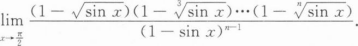
根据题意回答问题。
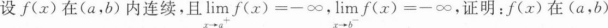
内有最大值.
根据题意回答问题。
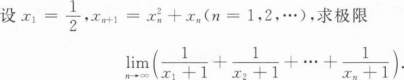
根据题意回答问题。
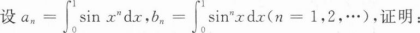
0≤bn≤an;
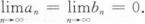
设f(x)在[a,b]上可导,且|f'(x)|<1,当x∈[a,b]时,有a<f(x)<b,F(x)=
[x+f(x)]/2,证明:
存在x*∈(a,b),使得F(x*)=x*;