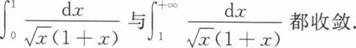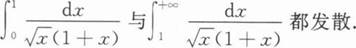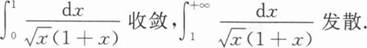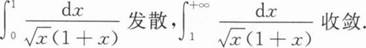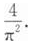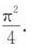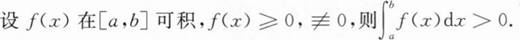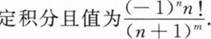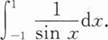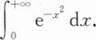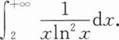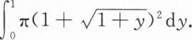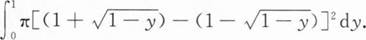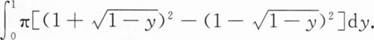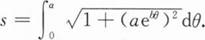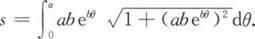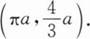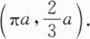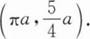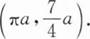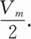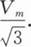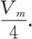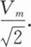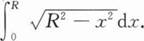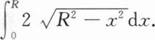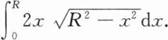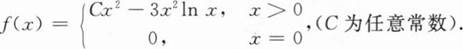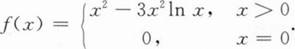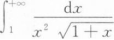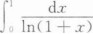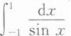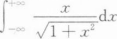下列结论中正确的是
π/2
2/π
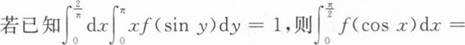
下列命题中有一个正确的是
设f(x)在[a，b]可积，g(x)在[a，b]不可积则f(x)+g(x)在[a，b]不可积
设f2(x)在[a，b]可积，则f(x)在[a，b]可积
设f(x)在[a，b]连续，则下列结论中正确的个数为
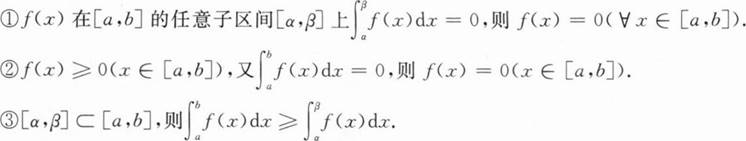
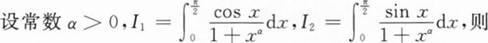
下列用牛顿一莱布尼茨公式计算定积分的做法中，错误的做法一共有
反常积分且发散
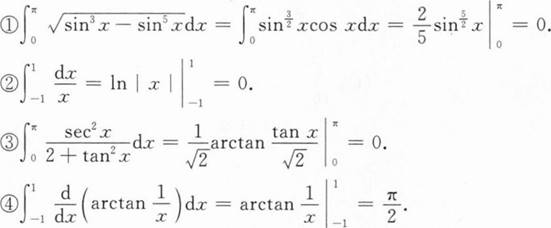
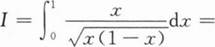
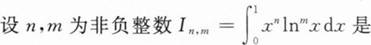
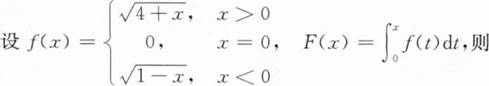
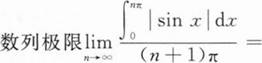
下列反常积分发散的是
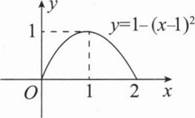
由曲线y=1-(x-1)2及直线y=0围成图形绕y轴旋转而成立体的体积V是
旋轮线x=a(t-sin t)，y=a(1-cos t)(0≤t≤2π)的质心是
峰值为Vm，周期为T的三角形波的电压平均值为
半圆形闸门半径为R(米)，将其垂直放入水中，且直径与水面齐．设ρg=1．若坐标原点取在圆心，x轴正向朝下，则闸门所受压力p为
设f(x)在[0，+∞)上连续，在(0，+∞)内有连续导数且 则
可得
f(x)=Cx2-3x2ln(1+x)(x∈[0，+∞))，(C为任意常数)．
f(x)=x2-3x2ln(1+x)(x∈[0，+∞))．
下列反常积分收敛的是（）．
设f(x)二阶可导，则下列结论正确的是（）．
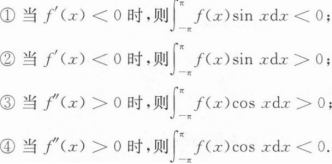
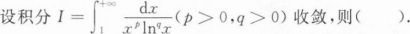
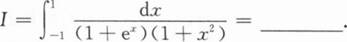
根据题意回答问题。
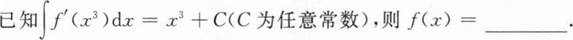
根据题意回答问题。
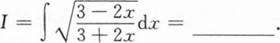
根据题意回答问题。
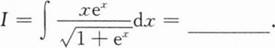
根据题意回答问题。
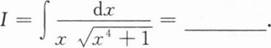
根据题意回答问题。
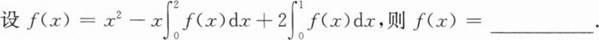
根据题意回答问题。
根据题意回答问题。
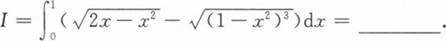
根据题意回答问题。
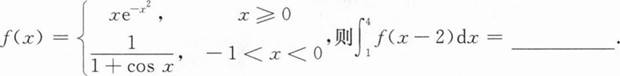
根据题意回答问题。
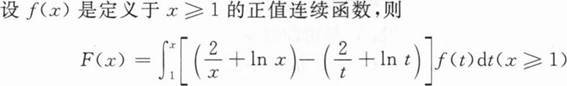
的极小值点是x=______．
根据题意回答问题。
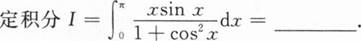
根据题意回答问题。
在曲线y=x2(0≤x≤1)上取一点(t，t2)，(0<t<1)，设A1是曲线y=x2(0≤x≤1)，直线y=t2和x=0围成的面积；A2是由曲线y=x2(0≤x≤1)直线y=t2和x=1围成的面积，则t取______时，A=A1+A2取最小值．
根据题意回答问题。
摆线x=a(t-sint)，y=a(1-cos t)(0≤t≤2π)与x轴围成图形绕y=2a旋转一周而得旋转体的体积V=______．
根据题意回答问题。
设有曲线
，过原点作其切线，则以曲线、切线及x轴所围成平面图形绕x轴旋转一圈所得到的表面积为______．
根据题意回答问题。
设对任意x，有f(x+4)=f(x)，且f'(x)=1+|x|，x∈[-2，2]，f(0)=1，则f(9)=_____.
根据题意回答问题。
(Ⅰ)
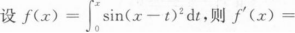
根据题意回答问题。
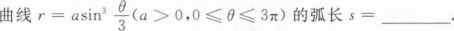
根据题意回答问题。
由曲线y=lnx与两直线y=(e+1)-x及y=0所围平面图形的面积S=
根据题意回答问题。
根据题意回答问题。
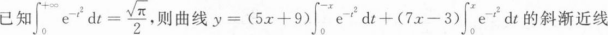
方程为_______.
根据题意回答问题。
求下列积分：
根据题意回答问题。
求下列积分：
根据题意回答问题。
求下列积分：
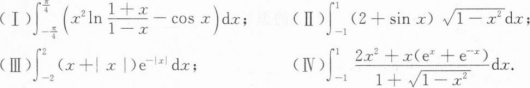
根据题意回答问题。
求下列积分：
(Ⅲ)
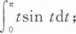
(Ⅳ)
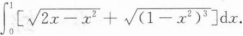
根据题意回答问题。
计算下列积分： (Ⅰ)
(Ⅱ)
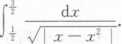
根据题意回答问题。
设f(x)在[0，π]上有二阶连续导数，f(0)=2，f(π)=1，计算
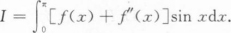
根据题意回答问题。
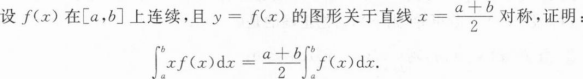
根据题意回答问题。
根据题意回答问题。
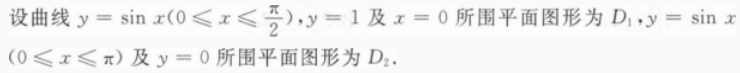
(Ⅰ)
(Ⅱ)
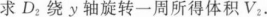
根据题意回答问题。
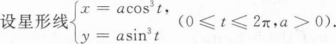
求所围面积A；
求弧长L；
求绕x轴旋转一周所得体积V和表面积S．
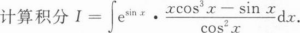
根据题意回答问题。
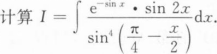
根据题意回答问题。
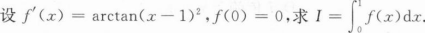
根据题意回答问题。
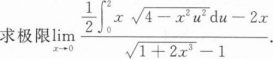
根据题意回答问题。
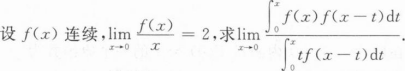
根据题意回答问题。
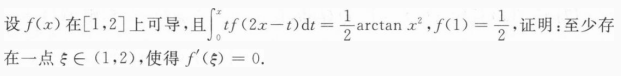
根据题意回答问题。
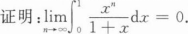
根据题意回答问题。
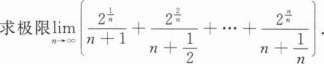
根据题意回答问题。
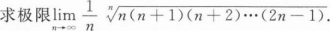
根据题意回答问题。
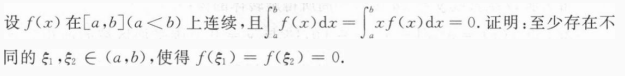
根据题意回答问题。
设y=f(x)在[0，1]上是非负连续函数．
证明：存在x0∈(0，1)，使得在[0，x0]上以f(x0)为高的矩形面积，等于在[x0，1]上以y=f(x)为曲边的曲边梯形面积；
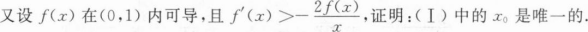
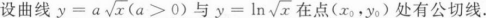
求常数a及点(x0，y0)；
求两曲线与x轴所围图形绕x轴旋转一周所得旋转体的体积．
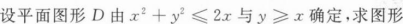
D绕直线x=2旋转一周所得旋转体的体积．
根据题意回答问题。
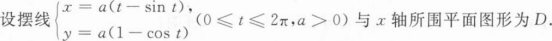
求D绕x轴，y轴各旋转一周所得旋转体的体积；
求D绕直线y=2a旋转一周所得旋转体的体积．
将半径为R的球沉入水中，它与水面相切，设球的密度与水的密度相等，现将球从水中取出，问至少需要做功多少?
根据题意回答问题。
设f(c)在[a，b]上连续，在(a，b)内可导，f'(x)>0，证明：存在唯一的ξ∈(a，b)， 使得y=f(x)与y=f(ξ)，x=a所围图形的面积S1，和y=f(x)与y=f(ξ)，x=b所围图形的面积S2，满足S1=3S2．
根据题意回答问题。
写出S1+S2关于t的函数表达式；
证明：S1+S2有最小值．
设y=f(x)在[0，+∞)上非负连续，曲边梯形 D(t)={(x，y)|0≤x≤t，0≤y≤f(x)}， D(t)所围图形的面积s(t)=tet，D(t)绕直线x=t旋转一周所得旋转体的体积为V(t)，求V(t)的表达式．
根据题意回答问题。
