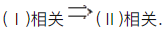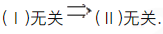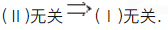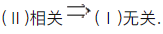设向量组Ⅰ:α1,α2,…,αr可由向量组Ⅱ:β1,β2,…,βs线性表示,下列命题中正确的是
设α1,α2,α3,α4是三维非零向量,则下列命题中正确的是
①若β不能由α1,α2,α3线性表示,则α1,α2,α3线性相关.②若α1,α2,α3线性相关,则β不能由α1,α2,α3线性表示.③若β能由α1,α2,α3线性表示,则α1,α2,α3线性无关.④若α1,α2,α3线性无关,则β能由α1,α2,α3线性表示.以上的命题正确的是
设矩阵A=[α1,α2,α3,α4],其中α1,α2,α3线性无关,α1,α2,α3,α4线性相关,A经过初等行变换变为矩阵B=[β1,β2,β3,β4].则
已知四维向量组α1,α2,α3,α4线性无关,且向量β1=α1+α3+α4,β2=α2-α4,β3=α3+α4,β4=α2+α3,β5=2α1+α2+α3,则r(β1,β2,β3,β4,β5)=
当向量组α1,α2,…,αs线性相关时,使等式k1α1+k2α2+…+ksαs=0成立的常数k1,k2,…,ks是
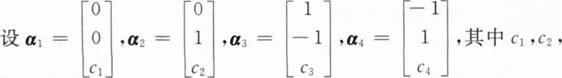
c3,c4为任意常数,则下列向量组线性相关的是
向量组α1,α2,…,αs线性无关的充分必要条件是
设向量组(Ⅰ):α1,α2,…,αs;向量组(Ⅱ):α1,α2,…,αs,αs+1,…,αs+t,则正确命题是
已知四维列向量组α1,α2,α3,α4线性无关,则下列向量组中线性无关的是
已知3维向量α1,α2,α3线性无关,则下列向量组中线性无关的是
已知β1=(4,-2,a)T,β2=(7,b,4)T可由α1=(1,2,3)T,α2=(-2,1,-1)T线性表示,则
如果向量组α1,α2,…,αs的秩为r则下列命题中正确的是
已知α1,α2,α3线性无关,则线性无关的向量组是
设α1=(a1,a2,a3)T,α2=(b1,b2,b3)T,α3=(c1,c2,c3)T,其中ai2+bi2≠0(i=1,2,3),则三条直线aix+biy+ci=0(i=1,2,3)恰好仅交于一点的充要条件是().
设α1,α2,α3均为3维向量,则对任意常数k和μ,向量组α1+kα3,α2+μα3线性无关是向量组α1,α2,α3线性无关的().
设A是m×n矩阵,α1,α2,…,αt是n维列向量,向量组(Ⅰ)α1,α2,…,αt,(Ⅱ)Aα1, Aα2,…,Aαt,则正确的是().
设向量α1,α2,α3满足k1α1+k2α2+k3α3=0,k1,k2,k3为常数,且k1k3≠0,
则().
设n维向量组(Ⅰ)α1,α2,…,αk(k<n)线性无关,则n维向量组(Ⅱ)β1,β2,…,βk也线性无关的充要条件是().
设A,B均是m×n矩阵,则Ax=0与Bx=0同解的充要条件是().
已知向量组α1=(a,0,b)T,α2=(0,a,c)T,α3=(f,b,0)T线性相关,则a,b,c必满足_____.
根据题意回答问题。
已知向量组α1=(1,2,-1,1)T,α2=(2,0,t,0)T,α3=(0,-4,5,t)T线性无关,则t的取值为.
根据题意回答问题。
已知α1,α2,α3线性无关,若α1+2α2+α3,α1+aα2,3α2+α3线性相关,则a=
根据题意回答问题。
已知向量β=(1,a,-1)T可以由α1=(a+2,7,1)T,α2=(1,-1,2)T线性表出,
则a=.
根据题意回答问题。
已知向量组β=(1,0,1,2)T,α1=(1,1,3,1)T,α2=(2,-1,a,5)T线性相关,则a=______.
根据题意回答问题。
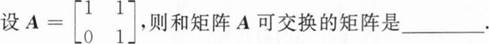
根据题意回答问题。
已知α1,α2,…,αt是齐次方程组Ax=0的基础解系,β不是Ax=0的解,证明β+α1,β+α2,…,β+αt线性无关.
根据题意回答问题。
已知向量α1=(1,2,3)T,α2=(2,-1,1)T,α3=(-2,k,4)T线性相关,则k=
根据题意回答问题。
设向量组(Ⅰ)α1,α2,α3,(Ⅱ)α1,α2,α3,α4,(Ⅲ)α1,α2,α3,α5,且r(Ⅰ)=r(Ⅱ)=3,r(Ⅲ)=4,证明:向量组α1,α2,α3,α5-α4的秩为4.
根据题意回答问题。
设A是3阶方阵,α1,α2为A的分别属于特征值-2,1的特征向量,且Aα3=α2+α3,
证明:α1,α2,α3线性无关.
根据题意回答问题。
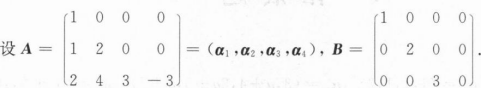
求向量组α1,α2,α3,α4的一个极大线性无关组;
求可逆矩阵P3×3,Q4×4,使得PAQ=B.
设向量组α1=(1,0,1)T,α2=(0,1,1)T,α3=(1,3,5)T不能由向量组β1=(1,1,1)T,β2=(1,2,3)T,β3=(3,4,a)T线性表示,求a的值,并将β1,β2,β3用α1,α2,α3线性表示.
根据题意回答问题。
设A=(α1,α2,α3),其中α1=(1,0,1)T,α2=(1,1,2)T,α3=(1,2,以)T,B=(β1,β2),其中β1=(-1,2,1)T,β2=(1,0,6)T.
问a,b为何值时,β1,β2不能同时由α1,α2,α3线性表示;
问a,b为何值时,β1,β2可同时由α1,α2,α3线性表示,并求表达式.
设n维向量组α1,α2,…,αk(k<n)线性无关,且ak-1=λ1α1+λ2α2+…+λkαk,λi≠0,i=1,2,…,k,证明:α1,α2,…,αk,αk+1中任何k个向量都线性无关.
根据题意回答问题。
设A是3阶方阵,A的特征值为λ1=1,λ2=2,λ3=3,对应的特征向量分别为α1=(1,1,1)T,α2=(1,2,4)T,α3=(1,3,9)T,另一向量β=(1,1,3)T.
将β用α1,α2,α3线性表示;
求Anβ(n为正整数).
设A是m×n矩阵,α1与α2是非齐次线性方程组Ax=b的两个不同解.
证明:α1,α1-α2线性无关;
若β是Ax=0的一个非零解向量,r(A)=n-1,证明:β,α1,α2线性相关.
设A是3阶矩阵,αi(i=1,2,3)是3维非零列向量,且Aαi=iαi(i=1,2,3),α=α1+α2+α3,证明:α,Aα,A2α线性无关.
根据题意回答问题。
设向量组α1=(1,1,1,2)T,α2=(3,a+4,2a+5,a+7)T,α3=(4,6,8,10)T,α4= (2,3,2a+3,5)T,α=(0,1,3,6)T.
求向量组α1,α2,α3,α4的秩及其一个极大线性无关组;
若口不能由α1,α2,α3,α4线性表示,求a,b的取值.