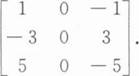已知A是三阶矩阵,满足A2+2A=O,若|A+3E|=3,则|2A+E|=

B的特征值是
三阶矩阵A的特征值全为零,则必有
设三阶矩阵A的特征值是0,1,-1,则下列命题中不正确的是
下列矩阵中,不能相似对角化的矩阵是
设α=(a1,a2,a3)T是单位向量,矩阵A=2E+3ααT,则A相似于
设A是四阶矩阵,α1,α2,α3是3维线性无关的列向量,且有Aα1=3α1,Aα2=3α2,
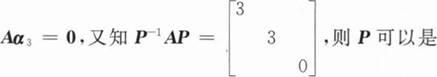
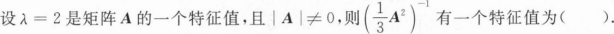

设A为3阶方阵,A的三个特征值为1,1,2,α1,α2,α3分别为对应的三个特征向量,则().
设A,B是n阶可逆矩阵,且A-1~B-1,则下列结果 ①AB~BA②A~B③A2~B2④AT~BT 中正确的个数为().
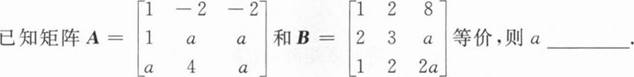
根据题意回答问题。
已知A是三阶实对称矩阵,λ1=1和λ2=2是A的2个特征值,对应的特征向量分别是α1=(1,a,-1)T和α2=(1,4,5)T.若矩阵A不可逆,则Ax=0的通解是____.
根据题意回答问题。

根据题意回答问题。
已知三阶矩阵A的特征值是1/2,1/3,1/4.三阶矩阵B满足关系式A-1BA=6A+BA,则矩阵B的特征值是____.
根据题意回答问题。

根据题意回答问题。
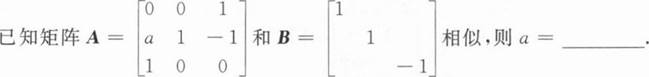
根据题意回答问题。
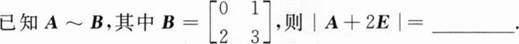
根据题意回答问题。

的逆矩阵的特征向量,那么α在矩阵A中对应的特征值是______.
根据题意回答问题。
设A是三阶矩阵,α1,α2,α3是三维线性无关的列向量,且Aα1=α2+α3,Aα2=α1+α3,Aα3=α1+α2,则和A相似的矩阵是______.
根据题意回答问题。
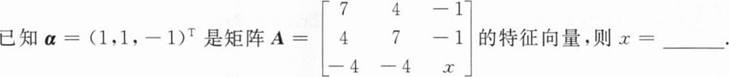
根据题意回答问题。
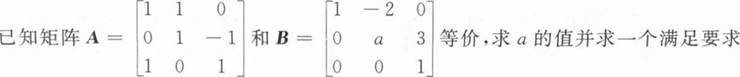
的可逆矩阵P和Q使PAQ=B.
根据题意回答问题。
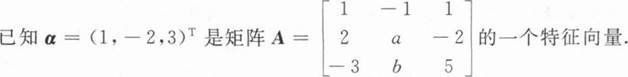
求a,b的值.
判断A能否相似对角化?如能则求可逆矩阵P使P-1AP=A,若不能则讲清理由.
设n阶方阵B=AA*,则B的特征值为____.
根据题意回答问题。
设方阵A满足A2+2A+E=0,则A有特征值____.
根据题意回答问题。

根据题意回答问题。
设3阶矩阵A的特征值为0,1,2,B=A3-2A2,则r(B)=_____.
根据题意回答问题。

求A的全部特征值和特征向量;
求可逆矩阵P,使得P-1AP为对角矩阵;
求正交矩阵Q,使Q-1AQ为对角矩阵.
设A是3阶矩阵,α1,α2,α3是线性无关的3维列向量,且Aα1=α1+α2+α3, Aα2=2α2+α3,Aα3=2α2+3α3.
求A的全部特征值;
求可逆矩阵P及A,使得P-1AP=A,并计算|A-2E|.

求a的值;
求可逆矩阵P,使得P-1AP为对角矩阵.
设3阶实对称矩阵A的特征值为λ1=λ2=1,λ3=-1,α1=(1,1,1)T,α2=(2,2,1)T 是λ1=λ2=1对应的特征向量.
求A的属于λ2=-1的特征向量;
求矩阵A.
(Ⅰ)设A是n阶实对称矩阵,且A2=A,r(A)=r(r<n),计算|3E-A|;
(Ⅱ)设A是n阶矩阵,且A2=A,r(A)=r(r<n),计算|3E-A|.
根据题意回答问题。
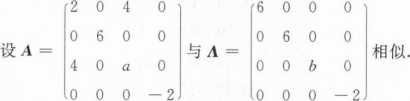
求a,b的值;
求一个正交矩阵P,使得P-1AP=A.
(Ⅰ)设A与B是n阶方阵,A可逆,且A~B,证明:A*~B*;
(Ⅱ)若A~B,证明:存在可逆矩阵P(非数量矩阵),使得AP~BP.
根据题意回答问题。
已知A=(α1,α2,α3)是3阶可逆矩阵,B是3阶矩阵,且BA=(α1,-4α3,-α2).
求B的全部特征值;
求可逆矩阵P和对角矩阵A,使得P-1BP=A.
设A是,n(n≥2)阶矩阵,α1,α2,…,αn。是n维列向量,且Aα1=α2,Aα2=α3,…, Aαn-1=αn,Aan=0,αn≠0.
证明:α1,α2,…,αn线性无关;
求可逆矩阵P及三角矩阵B,使得P-1AP=B.
设α=(a1,a2,…,an)T,β=(b1,b2,…,bn)T均为非零列向量,A=αβt.
求A的全部特征值;
问αtβ满足什么条件时,A可以相似于对角矩阵A,并求可逆矩阵P,使P-1AP=A.

求可逆矩阵P及对角矩阵A,使得P-1AP=A;
求r(A*).
设α,β为3维单位列向量,且αtβ=0,记A=αβt+βαt.
证明:A相似于对角矩阵;
若存在3维列向量γ≠0,使得Aγ=0,记P=(γ,2(α+β),β-α),求P-1AP.
设A,B均是n阶矩阵.
证明:AB与BA有相同的特征值;
证明:AB与BA有相同的特征值;
设A是2阶矩阵,α是非零向量,且α不是A的特征向量.
证明:α,Aα线性无关;
记P=(α,Aα),若A2α-2Aα=8α,证明:A相似于对角矩阵,并求P-1AP.