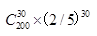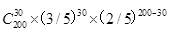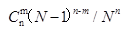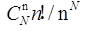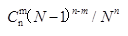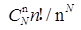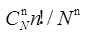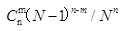某公司有9名工程师，张三是其中之一，从中任意抽调4人组成攻关小组，包括张三的概率是（）。

在10道备选试题中，甲能答对8题，乙能答对6题。若某次考试从这10道备选题中随机抽出3道作为考题，至少答对2题才算合格，则甲乙两人考试都合格的概率是（）。

若将10只相同的球随机放入编号为1、2、3、4的四个盒子中，则每个盒子不空的投放方法有（）种。

若以连续掷两枚骰子分别得到的点数a与b作为点M的坐标，则点M落入圆x²＋y²＝18内（不含圆周）的概率是（）。

若从原点出发的质点M向x轴的正向移动一个和两个坐标单位的概率分别是2/3和1/3。质点移动3个坐标单位，到达x＝3的概率是（）。

某乒乓球男子单打决赛在甲乙两选手间进行比赛用7局4胜制。已知每局比赛甲选手战胜乙选手的概率为0.7，则甲选手以4：1战胜乙的概率为（）。

10件产品中有3件次品，从中随机抽出2件，至少抽到一件次品的概率是（）。

设袋中有4只白球和2只黑球，现从袋中无放回地依次摸出2只球，则这2只球都是白球的概率为（）。

设袋中有10个相同的球，依次编号为1，2，…，10，每次从袋中任取一球，取后不放回，第5次取到1号球的概率为（）。

袋中有4个红球，6个黑球，从中有放回地摸球3次，则前两次摸到黑球，第3次摸到红球的概率为（）。

袋中有4个红球，6个黑球，则从中有放回地摸球200次中红球出现30次的概率为（）。

从5双不同的鞋子中任取4只，则取得的4只鞋中至少有2只配成一双的概率（）。

把4个球放到3个杯子中去，其中假设每个杯子可放任意多个球。则第1、2个杯子中各有两个球的概率为（）。

设随机变量X服从[2，5]上的均匀分布，现在对X进行三次独立重复的观测，则至少有两次观测值大于3的概率为（）。

6位同学参加百米赛跑初赛，赛场共有6条跑道，其中甲同学恰好被排在第一道，乙同学恰好被排在第二道的概率为（）。

从0、1、2、…、9这十个数字中任取不同的三个数字，三个数字之和等于10的概率为（）。

某产品的次品率p＝0.05，对该产品进行重复抽样检验，选取4个样品。求其中恰好有两个次品的概率是______，其中至少有两个次品的概率是______。（）（保留4个有效数字）

（）。 （1）n²－7n＋12＝0 （2）n²－10n＋24＝0

命中来犯敌机的概率是99%（）。 （1）每枚导弹命中率为0.6 （2）至多同时向来犯敌机发射4枚导弹

有n个人，每个人都以同样的概率1/N被分配在N（n≤N）间房中的每一间中。 某指定n间房中各有一人的概率为（）。

有n个人，每个人都以同样的概率1/N被分配在N（n≤N）间房中的每一间中。 恰有n间房，其中各有一人的概率为（）。

有n个人，每个人都以同样的概率1/N被分配在N（n≤N）间房中的每一间中。 某指定一间房中恰有m个人的概率为（）。

先后抛掷3枚均匀的壹分、贰分、伍分硬币。 一共可能出现多少种不同结果？（）

某地区有5个工厂，由于用电紧缺，规定每个工厂在一周内必须选择某一天停电（选哪一天是等可能的）。假定工厂之间的选择互不影响。 5个工厂均选择星期日停电的概率是（）。

某地区有5个工厂，由于用电紧缺，规定每个工厂在一周内必须选择某一天停电（选哪一天是等可能的）。假定工厂之间的选择互不影响。 至少有两个工厂选择同一天停电的概率是（）。