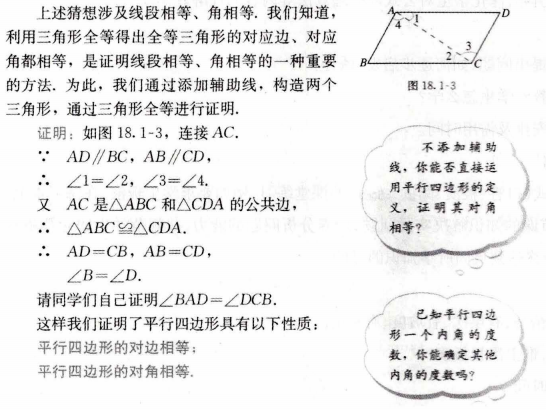
【初中】1.题目：平行四边形的性质 2.内容： 由平行四边形的定义，我们知道平行四边形的两组对边分别平行，除此之外，平行四边形还有什么性质呢？ 探究： 根据定义画一个平行四边形，观察它，除了“两组对边分别平行”外，它的边之间还有什么关系？它的角之间有什么关系？度量一下，和你的猜想一致吗？ 通过观察和度量，我们猜想：平行四边形的对边相等；平行四边形的对角相等。下面我们对它进行证明。

3.基本要求： （1）证明思路明确、清晰； （2）请在10分钟内完成试讲内容； （3）要有合适的板书； （4）设置情景教学。

【初中】1.题目：正方形性质的应用 2.内容： 例5 求证：正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形。 已知：如图18.2-12，四边形ABCD是正方形，对角线AC，BD相交于点O。 求证：△ABO，△BCO，△CDO，△DAO。是全等的等腰直角三角形。

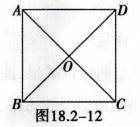
证明：∵四边形ABCD是正方形， ∴AC=BD，AC⊥BD，A0=B0=C0=D0。 ∴△ABO，△BCO，△CDO，△DAO都是等腰直角三角形，并且 △ABO≌△BCO≌△CDO≌△DAO。 3.基本要求： （1）书写完整的证明过程； （2）试讲10分钟； （3）要有合适的板书。

【高中】1.题目：等比数列 2.内容：

3.基本要求： （1）讲解等比数列的概念； （2）教学过程中注意师生间的交流互动，有适当的提问环节； （3）要求配合教学内容有适当的板书设计； （4）请在10分钟内完成试讲内容。

【高中】1.题目：指数函数图象和性质的应用 2.内容：

3.基本要求： （1）试讲时间10分钟左右； （2）讲解要目的明确、条理清楚、重点突出； （3）根据讲解的需要适当板书； （4）指导学生利用指数函数的性质比较两个数的大小。