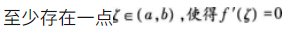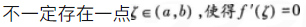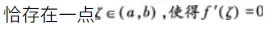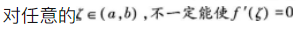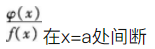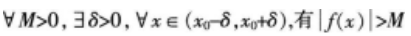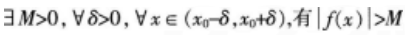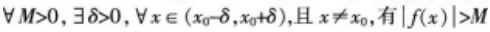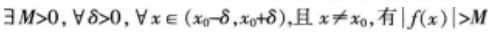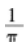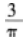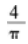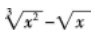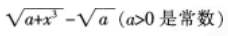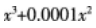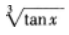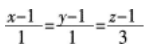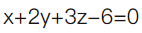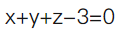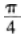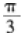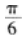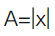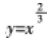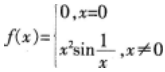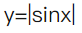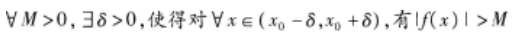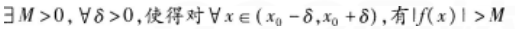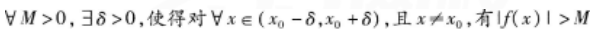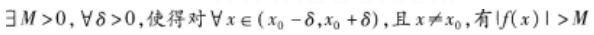设三次多项式函数
则f(x)的极大值点为( )
的值域区间为( )
若f(x)在[a，b]上连续，在(a，b)可导且f(a)=f(b)，则( )
由曲线y=x2，y=x3围成的封闭图形的面积为( )
曲线
的斜渐近线方程为( )
直线
与x轴交于点P，已知点P在圆2+(y+2)2=25内，过点P的一条直径被点P分为两段，则较短的一段与较长的一段的比值为( )
设f(x)，g(x)在x=x0处均不连续，则在x=x0处( )
的值为( )
设曲线
则该曲线( )
设f(x)为不恒等于零的奇函数，且f'(0)存在，则关于函数
下列正确的是( )。
设f(x)在x=a处连续，φ(x)在x=a处间断，又f(x)≠0，则( )
f[φ(X)]在x=a处间断
f[φ(X)]在X=a处间断
[φ(x)]2在x=a处间断
已知
则在点x=a处( )
函数
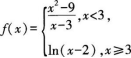
在x=3处的极限是( )
如下所示4个命题中假命题的个数为( )
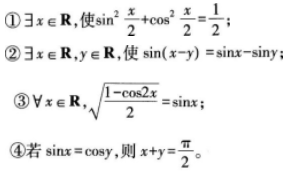
当x→0时，下列哪一个无穷小是x的三阶无穷小?()
曲线x=t，y=t2,z=t3在点(1，1，1)处的法平面方程是()。
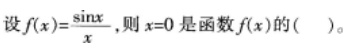
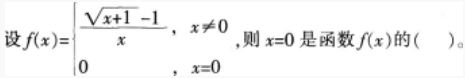
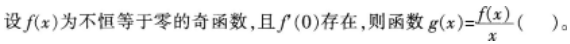
下列函数在x=0处可导的是( )。
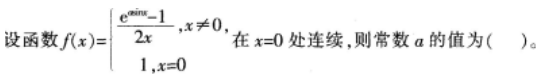
下列说法正确的是（ ）
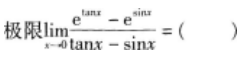
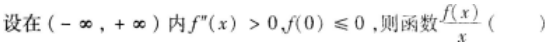
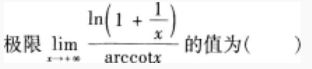
设ƒ(x)在(-∞，+∞)上有定义，则下列函数中为奇函数的是（ ）
求曲线
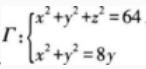
在xOy，yOz坐标面上的投影曲线的方程。
求曲线
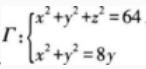
在xOy，yOz坐标面上的投影曲线的方程。
证明方程xex=1在区间(0，1)内有且仅有一个实数根。
证明方程xex=1在区间(0，1)内有且仅有一个实数根。
求
的间断点并判断其类型。
求
的间断点并判断其类型。
利用极限的定义证明
利用极限的定义证明
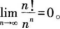
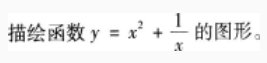
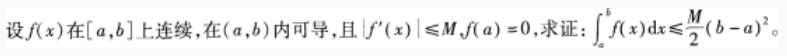
设ƒ(x)在[0，2a]上连续，且ƒ(0)=ƒ(2a)，证明：在[0，a]上至少存在一个ξ，使得ƒ(ξ)=ƒ(ξ+a)。
设ƒ(x)在[0，2a]上连续，且ƒ(0)=ƒ(2a)，证明：在[0，a]上至少存在一个ξ，使得ƒ(ξ)=ƒ(ξ+a)。
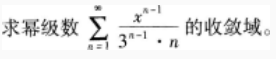
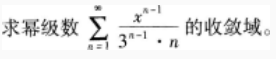
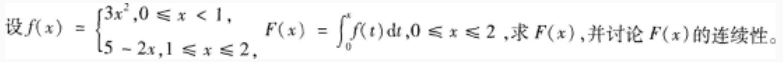
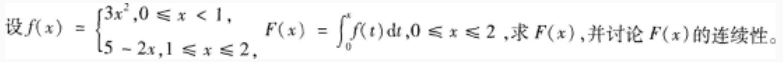
证明方程x5+x-1=0只有一个正根。
证明方程x5+x-1=0只有一个正根。
罗尔定理：设函数ƒ(x)满足条件：(1)在闭区间[a，b]上连续，(2)在开区间(a，b)内可导，(3)ƒ(a)=ƒ(b)，则在(a，b)内至少存在一点ξ，使得ƒ´(ξ)=0。证明这个定理并说明其几何意义。
罗尔定理：设函数ƒ(x)满足条件：(1)在闭区间[a，b]上连续，(2)在开区间(a，b)内可导，(3)ƒ(a)=ƒ(b)，则在(a，b)内至少存在一点ξ，使得ƒ´(ξ)=0。证明这个定理并说明其几何意义。
设f(x)，g(x)在[0，1]上的导数连续，且f(0)=0,f’(x)≥0，g'(x)≥0。证明：对任何a∈[0，1]，有
设f(x)，g(x)在[0，1]上的导数连续，且f(0)=0,f’(x)≥0，g'(x)≥0。证明：对任何a∈[0，1]，有
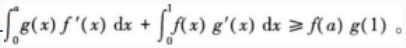
已知函数f(x)=ex+2x2-3x。 (1)求曲线y=f(x)在点(1,f(1))处的切线方程；
已知函数f(x)=ex+2x2-3x。 (1)求曲线y=f(x)在点(1,f(1))处的切线方程；
如下图所示，设0<a<b，函数ƒ(x)在[a，b]上连续，在(a，b)可微且ƒ(x)>0，ƒ(a)= ƒ(b)。设ι为绕原点O可转动的细棍(射线)，放手后落在函数ƒ(x)的图像上并支撑在点A(ζ，ƒ(ζ))上，从直观上看。
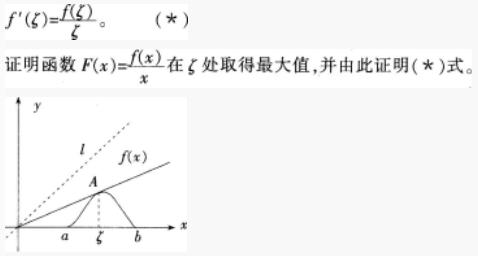
如下图所示，设0<a<b，函数ƒ(x)在[a，b]上连续，在(a，b)可微且ƒ(x)>0，ƒ(a)= ƒ(b)。设ι为绕原点O可转动的细棍(射线)，放手后落在函数ƒ(x)的图像上并支撑在点A(ζ，ƒ(ζ))上，从直观上看。
证明：连续的奇函数的一切原函数皆为偶函数；连续的偶函数的原函数中只有一个是奇函数。
证明：连续的奇函数的一切原函数皆为偶函数；连续的偶函数的原函数中只有一个是奇函数。
(1)将ƒ(x)的极大值M用a表示出来；(5分)
(2)将(1)中的M看作a的函数，求M取极小值时a的值。(5分)
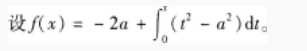
(1)将ƒ(x)的极大值M用a表示出来；(5分)
(2)将(1)中的M看作a的函数，求M取极小值时a的值。(5分)
