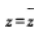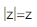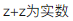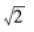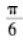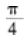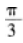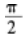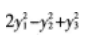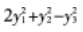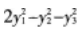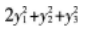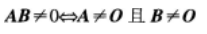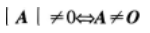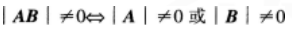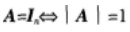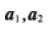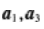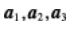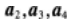等比数列{an}的各项为正数,且
使复数为实数的充分而不必要条件是( )
下列矩阵中,( )是正定矩阵。
设A是n阶矩阵,则|(2A)*|=( )
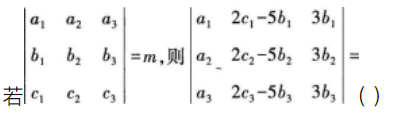
设a∈Z,且0<a<13,若512012+0能被13整除,则a=( )
设A是任一n阶矩阵,下列交换错误的是( )
若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )
已知直线y=x+2与抛物线y=ax2(a>0)交于A,B两点,0为抛物线的顶点,若
则a=( )
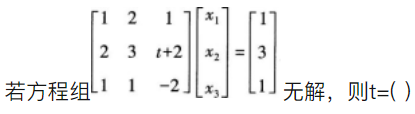
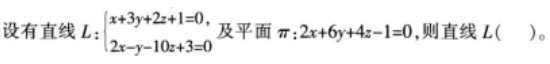
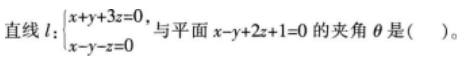
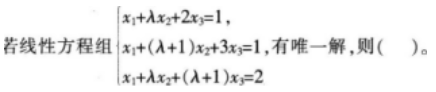
下列说法正确的是( )。
设P(A)=a,P(B)=b,P(A∪B)=c,则P(A-B)=( )。
曲面z=4-x2-y2上点P处的切平面平行于平面2x+2y+z-1=0,则点P的坐标是()。

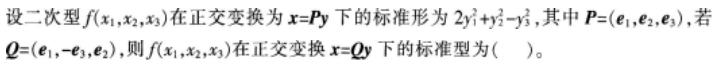

设A,B,A+B,A-1+B-1均为n阶可逆矩阵,则(A-1+B-1)-1=()。
则|A+B|的值为()。
设A,B是n阶方阵,则下列结论成立的是()。
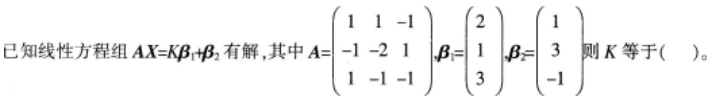
设λ1,λ2是矩阵A的两个不同的特征值,对应的特征向量分别为a1,a2,则a1,A(a1+a2)线性无关的充分必要条件是( )。
设A是m×n矩阵,如果m<n,则( )。
设a=(-1,2,-1),b=(1,-1,2),c=(3,-4,5),则( )。

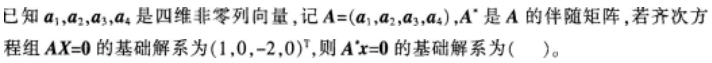


在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有( )
已知向量a≠0,以下条件中能推知b=c的是( )
已知2n阶行列式D的某一列元素及其余子式都等于a,则D=( )
已知向量口=(2,1),b=(X,Y)。
(1)若X∈{-1,0,1,2),Y∈{-1,0,1),求向量a//b的概率;
(2)若X∈[-1,2],Y∈[-1,1],求向量a,b的夹角是钝角的概率。
已知向量口=(2,1),b=(X,Y)。
(1)若X∈{-1,0,1,2),Y∈{-1,0,1),求向量a//b的概率;
(2)若X∈[-1,2],Y∈[-1,1],求向量a,b的夹角是钝角的概率。
在数列{an}中,a1=1,an+1=2an+2n。

在数列{an}中,a1=1,an+1=2an+2n。



已知向量a1=(1,3,2,0)T,a2=(7,0,14,3)T,a3=(2,-1,O,1)T,a4=(5,1,6,2)T,a5=(2,-1,4,1)T,求此向量组的一个极大无关组,并把其余向量用该极大无关组线性表示。
已知向量a1=(1,3,2,0)T,a2=(7,0,14,3)T,a3=(2,-1,O,1)T,a4=(5,1,6,2)T,a5=(2,-1,4,1)T,求此向量组的一个极大无关组,并把其余向量用该极大无关组线性表示。

设数列{an}的前n项和为Sn,且an+Sn=1(n∈N*)。
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=1,且2bn+1=bn+an(n≥1),求数列{bn}的通项公式。
设数列{an}的前n项和为Sn,且an+Sn=1(n∈N*)。
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=1,且2bn+1=bn+an(n≥1),求数列{bn}的通项公式。
如果数列{an}的前n项和
,求数列{an}的通项公式。
如果数列{an}的前n项和
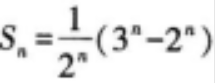
,求数列{an}的通项公式。
用克拉默法则解方程组:
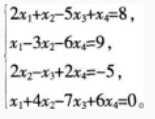
用克拉默法则解方程组:
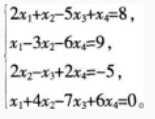
把向量β表示成a1,a2,a3,a4的线性组合,其中β=(1,2,1,1),a1=(1,1,1,1),a2=(1,1,-1,-1),a3=(1,-1,1,-1),a4=(1,-1,-1,1)。
把向量β表示成a1,a2,a3,a4的线性组合,其中β=(1,2,1,1),a1=(1,1,1,1),a2=(1,1,-1,-1),a3=(1,-1,1,-1),a4=(1,-1,-1,1)。
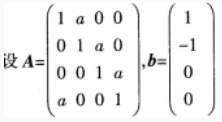
(1)求|A|;
(2)已知线性方程组AX=b有无穷多解,求a,并求AX=b的通解。

(1)求|A|;
(2)已知线性方程组AX=b有无穷多解,求a,并求AX=b的通解。
求出齐次线性方程组的一个基础解系并用它表示出全部解。
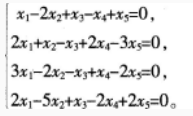
求出齐次线性方程组的一个基础解系并用它表示出全部解。
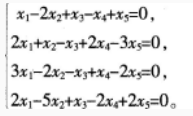
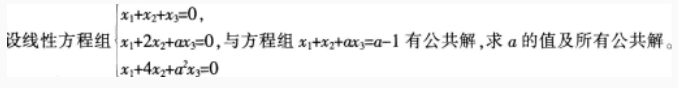
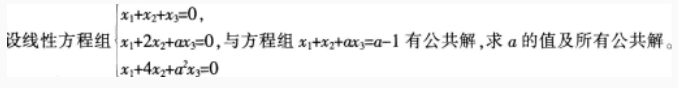


在一次军事演习中,某舟桥连接到命令要赶到某小河D岸为行进中的A部队架设浮桥。假设舟桥连到达D岸的时间服从7点到7点30分这时间段内的均匀分布,架设浮桥需要20分钟时间,A部队到达D岸的时间服从7点30分到8点整这时间段内的均匀分布,且舟桥连的到达时间和A部队的到达时间相互独立。
求A部队到达D岸时能立即过桥的概率。






设a1=(1,-1,2,4),a2=(0,3,1,2),a3=(3,0,7,14),a4=(1,-1,2,0),a5=(2,1,5,6)。
(1)证明a1,a2线性无关;
(2)把a1,a2扩充成一极大线性无关组。

(1)当A取何值时有解,并求其解;
(2)当A取何值时无解;
(3)当A取何值时有唯一解,说明理由。



(1)试求a的值;
(2)求正交矩阵Q,使QTAQ为对角矩阵。