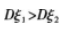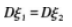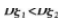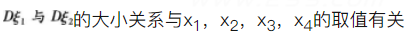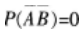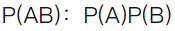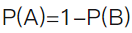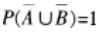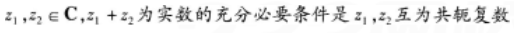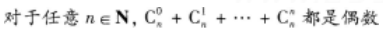已知随机变量x与y有相同的不为0的方差,则X与Y,的相关系数ρ=1的充要条件是( )
设随机变量X1,X2,…,Xn(n>1)独立分布,且方差ó2>0,记
的相关系数为( )

设随机变量X服从正态分布N(μ,σ2),则随着σ的增大,概率P{|x-μ|<σ}应该()。
某人向同一目标独立重复射击,每次射击命中目标的概率为P(0<p<1),则此人第四次射击恰好第二次命中目标的概率为( )。
设事件A与事件B互不相容,则( )。
下列命题中,假命题为( )
为拉动经济增长,某市决定新建一批重点工程,分为基础设施工程、民生工程和产业建设工程三类。这三类工程所含项目的个数分别占总数的1/2,1/3,1/6。现有三名工人独立地从中任选一个项目参与建设。
求他们选择的项目所属类别互不相同的概率;
记ξ为3人中选择的项目属于基础设施工程或产业建设工程的人数,求ξ的分布列及数学期望。
某单位招聘面试,每次从试题库调用一道试题,若调用的是A类型试题,则使用后该试题回库,并增补一道A类型试题和一道B类型试题入库,此次调题工作结束;若调用的是B类型试题,则使用后该试题回库,此次调题结束。试题库中现有n+m道试题,其中有n道A类型试题和m道B类型试题,以x表示两次调题工作完成后,试题库中A类型试题数量。
求X=n+2的概率;
设n=m,求X的分布列和均值。
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3道题,每人答对其中2道题就停止作答,即闯关成
求甲、乙至少有一人闯关成功的概率;
设甲答对题目的个数为ξ,求ξ的分布列及数学期望。
袋中有1个红球、2个黑球与3个白球,现有放回地从袋中取两次,每次取一个球,以X,Y,Z分别表示两次取球所取得的红球、黑球与白球的个数。
求P|X=1|Z=0};
求二维随机变量(X,Y)的概率分布。
已知连续型随机变量X的概率密度为
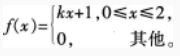
求:(1)k;(2)分布函数F(x);(3)P(1.5≤x≤2.5)。
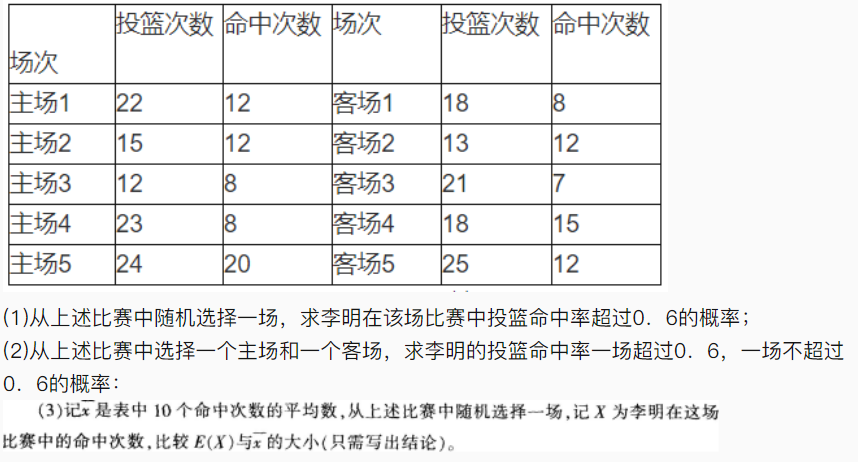
李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):

甲、乙、丙三车间加工同一产品,加工量分别占总量的25%,35%,40%,次品率分别为0.03,0.02,0.01。现从所有产品中取出一件,试求:
该产品是次品的概率;
若检查结果显示该产品是次品,则该产品是乙车间生产的概率是多少?
在空战训练中甲机先向乙机开火,击落乙机的概率为0.2;若乙机未被击落,就进行还击,击落甲机的概率是0.3;若甲机未被击落,则再攻击乙机,击落乙机的概率为0.4,求在这几个回合中:
甲机被击落的概率;
乙机被击落的概率。
玻璃杯成箱出售,每箱20只,假设各箱含0、1、2只残次品的概率分别为0.8、0.1和0.095。一顾客欲购一箱玻璃杯,在购买时,售货员随意取一箱,顾客开箱随机地察看四只,若无残次品,则买下该箱玻璃杯,否则退回,试求:
顾客买下该箱玻璃杯的概率P;
在顾客买下的一箱中,确实没有残次品的概率q。