简述新课程改革的教学观。
简述新课程改革的教学观。
组织者的含义是什么?教师的组织作用主要体现在哪些方面?
组织者的含义是什么?教师的组织作用主要体现在哪些方面?
《义务教育数学课程标准(2011年版)》指出:“数学思想蕴涵在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括,如抽象、分类、归纳、演绎、模型等。”
请简述,怎样让学生在学习过程中感悟数学思想。
《义务教育数学课程标准(2011年版)》指出教学活动是师生积极参与、交往互动、共同发展的过程。
教学中应该注意的几个关系是什么?
简述教学过程优化的要求以及教师在教学过程中应怎样实施优化。
简述教学过程优化的要求以及教师在教学过程中应怎样实施优化。
什么是几何直观?在教学中如何培养学生的几何直观观念?
什么是几何直观?在教学中如何培养学生的几何直观观念?
数形结合思想是一种重要的数学思想,它的实质就是根据数与形之间的对应关系,通过数与形的相互转化来解决问题。用数形结合思想解题能简化推理和运算,具有直观、快捷的优点。
请简要谈谈数形结合思想在解哪些类型的问题时可以发挥作用,使问题得到更好的解决。
数学课程标准各学段安排了“图形与几何”的学习内容来发展学生的空间观念,假如你在“图形与几何”知识教学时,将会从哪些方面去培养学生的空间观念?
数学课程标准各学段安排了“图形与几何”的学习内容来发展学生的空间观念,假如你在“图形与几何”知识教学时,将会从哪些方面去培养学生的空间观念?
如何让学生养成勇于质疑的习惯,形成实事求是的态度?
如何让学生养成勇于质疑的习惯,形成实事求是的态度?
“巩固与发展相结合”是数学教学的基本原则。谈谈“巩固”与“发展”的关系,教师在教学过程中怎样做到在发展的过程中进行巩固。
“巩固与发展相结合”是数学教学的基本原则。谈谈“巩固”与“发展”的关系,教师在教学过程中怎样做到在发展的过程中进行巩固。
某教师在进行二元一次方程教学时,给学生出了如下一道练习题: 已知a,b是方程X2+(k-1)x+k+1=0的两个根且a,b是某直角三角形的两条直角边,其斜边长等于1,求k的值。某学生的解答过程如下: 解:∵a,b是方程x2+(k-1)x+k+1=0的两个根, ∴a+b=1-k,ab=k+1,又由已知得:a2+b2=1, ∴(a+b)2-2ab=1,即k2-4k-2=0,解得
指出该生解题过程中的错误,分析其错误原因;
给出你的正确解答;
指出你解题所运用的数学思想方法。
用火柴搭正方形,搭l个正方形需要4根火柴棒。

(1)按图示方式搭2个正方形需要几根火柴棒?搭3个正方形需要几根火柴棒? (2)搭10个正方形需要几根火柴棒? (3)100个正方形呢?你是怎样得到的? (4)如果用x表示搭正方形的个数,那么搭x个这样的正方形需要多少根火柴棒?与同伴交流。
请试着解第(4)个问题,尽可能有多种解法;简要分析“多样化”的解题策略设计的作用;
一个好的课堂活动可以促进学生多方面发展。结合本案例,简要论述数学教学中应如何体现教材学习目标。
下面是某位老师引入“负数”概念的教学片段。
师:我们当地7月份的平均气温是零上28℃,1月份的平均气温是零下3℃,问7月份的平均气温比1月份的平均气温高几度?如何列式计算?
生:用零上28℃减去零下3℃,得到的答案是31℃。师:答案没错,算式呢?
生:文字与数字混在一起,一点也不美观。
生:零上28℃,我们常说成28℃,可用28表示,但是零下3℃不能说成3℃呀!也就不能用3表示。
师:大家的发言很有道理,如何解决这一系列的矛盾呢?看样子有必要引入一个新数来表示零下3c℃。这时,零下3℃就可写成-3℃,-3就是负数。
对该教师情境创设的合理性作出解释;
在引入数学概念时,结合上述案例,说说教师创设情境要考虑哪些因素?
下面是教师讲授“探索并了解:过圆外一点所画的圆的两条切线长相等”的教学片段。 ①发现结论。在透明纸上画出如图1的图:设PA,PB是⊙O的两条切线,A,B是切点。让学生操作:沿直线OP将图形对折,启发学生思考,组织学生交流,使学生发现:PA=PB,∠APO=∠BP0。 ②证明结论。如图2,连结OA和OB。因为以和PB是(D0的切线,所以∠PAO=∠PBO=900,即△PAD与△PBD均为直角三角形。又因为OA=OB、OP=OP,所以△POA和APOB全等。于是有PA=PB,∠APO=A_BP0。
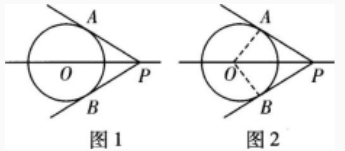
以上教学过程中,用到了哪两种推理方法;
结合案例简要阐述这两种推理方法的异同点及二者的作用;
写出你对上述教学过程的反思。
两位学生分别在实数范围内解方程x2+3x-4=0和x4+3x2-4=0。
第一位学生的解法如下:
x2+3x-4=0
(x-1)(x+4)=O
x-1=0或x+4=O
x1=1,x2=-4
第二位学生的解法如下:
x4+3x2-4=0
令x2=y.原方程变成y2+3y-4=O
(y-1)(y+4)=0
y1=1,y2=-4(舍去)
由x2=1得x=±1
这两位学生在解方程时分别运用了什么数学方法?
这些方法体现了数学思想是什么?请对该数学思想进行简要的描述。
如果用某种型号的代数计算器解以上两个方程,学生只需输入x2+3x-4=0和x4+3x2=0,在功能菜单中选择“解方程”然后按回车键。屏幕上就会出现方程的解。请问,如果从渗透数学思想方法的角度看,应如何在教学中让学生合理使用计算器?

判断学生1和学生2的解法正确吗?并说明理由。
如果你是该教师,如何完成后续的教学?
案例:阅读下列两个教师有关有理数乘方的教学片段。 甲教师导入的教学过程: 在大屏幕上依次呈现问题1(已知正方形的边长为a,则它的面积是多少?)和问题2(已知正方体的棱长为a,则它的体积是多少?)一待同学回答后,教师出示结果:边长为a的正方形的面积为a·a,简记作a2,读作a的平方(或二次方);棱长为a的正方体的体积为a·a·a,简记作a3,读作a的立方(或三次方)。 然后提出问题3:请大家动手折一折,一张报纸对折一次后,报纸有几层?如果对折两次、三次呢? 每一次对折后的层数与上一次对折层数的关系是什么?层数和对折的次数之间有什么关系?学生折叠并思考,教师巡视并提问一归纳:每一次对折后的层数都是上一次对折层数的2倍。概括层数和对折次数的关系及表示方法,填入下表中:
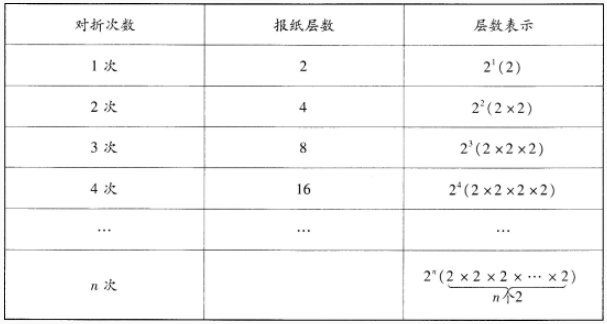
接下来,甲教师引出乘方的相关概念(大屏幕显示):一般地,把n个相同的因数a相乘的运算叫作乘方运算,把a·a·a·…·a(n个a)简记作an,读作a的n次方。 由此引出乘方、底数、指数、幂的概念。 乙教师导入的教学过程: 在大屏幕上呈现问题:某种细胞每过30分钟便由1个分裂成2个,经过5小时,这种细胞由1个可以分裂成多少个? 引导学生思考:分裂的次数与细胞的个数之间有什么关系?并完成下表:

由此,引出乘方、底数、指数、幂的概念。
分析甲、乙两位教师导入的相同点;
分析甲、乙两位教师导人中存在的问题。
针对“随机事件”起始课的教学。两位教师给出了如下教学设计片段:
【教师甲】
设置问题情境:下列问题哪些是必然发生的?哪些是不可能发生的?
①太阳从西边下山;②某人的体温是100℃;③a2+b2=-1(其中a,b都是实数);④水往低处流;⑤酸和碱反应生成盐和水;⑥三个人性别各不相同;⑦一元二次方程x2+2x+3=0无实数解。
引发思考:把上面的事件①、④、⑤、⑦称为必然事件,把事件②、③、⑥称为不可能事件,提问:什么是必然事件?什么又是不可能事件呢?它们的特点各是什么?
【教师乙】
在日常生活中我们会发现有些事件是可能发生的,有些事件是不可能发生的,有些事件是必然发生的.在数学中我们怎样定义事件发生的可能性呢?今天就来学习必然事件、不可能事件的概念。
请完成下列任务:
请分析两位教师引入“随机事件”概念设计方案的各自的特点;
请分析“随机事件”的重、难点;
在教学中,当引入一个新的数学概念之后,往往通过例题、习题加深对概念的理解。请针对“随机事件”概念,设计不同难度的两道例题和两道练习题,以加深学生对“随机事件”概念的理解。
“变量与函数”是初中数学教学中的重要内容,请完成下列任务:
在“变量与函数”起始课的“教学重点”设计中,有两种方案:
①强调认识变量、常量,用式子表示变量间关系。
②强调能指出具体问题中的常量、变量。初步理解存在一类变量可以用函数方式来刻画。你赞同哪种方案?简述理由。
给出y=4x+6以及4x+6=0,则指出哪个是函数,如果是函数,它的变量是什么?常量是什么?
为了让初中生充分认识“变量与函数”中“变量”的概念,作为教师应该对此有深刻的理解,请谈谈你对“变量”概念的认识。
下列是某教师针对“不等式的基本性质”一节设计的教学目标:
①知识与技能:掌握不等式的基本性质;经历类比、猜想、验证、发现不等式基本性质的探索过程,初步体会不等式与等式的异同。
②过程与方法:能说出一个不等式为什么可以从一种形式变形为另一种形式,发展其代数变形能力,养成步步有据、准确表达的良好学习习惯;进一步发展符号表达能力,以及提出问题、分析问题、解决问题的能力。
③情感态度与价值观:认识到通过观察、实验、类比可以获得数学结论,体验数学活动充满着探索性和创造性;在独立思考的基础上,积极参与对数学问题的讨论,敢于发表自己的观点,学会分享别人的想法和结果,并重新审视自己的想法,能从交流中获益。
请完成下列任务:
请根据教学目标写出这节课的教学重难点;
请根据教学目标①设计这节课的活动探索环节;
为巩固不等式的基本性质设计本节课的习题。


