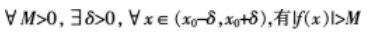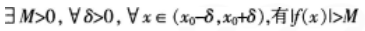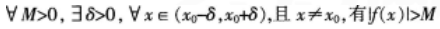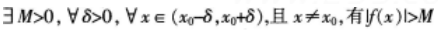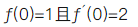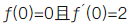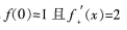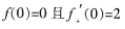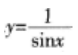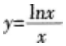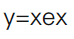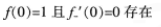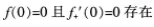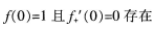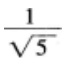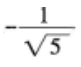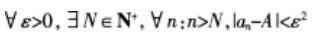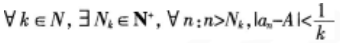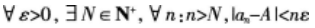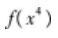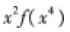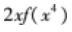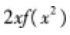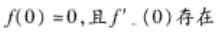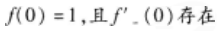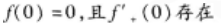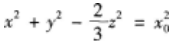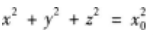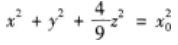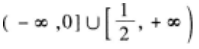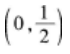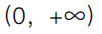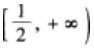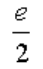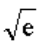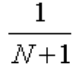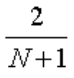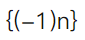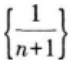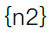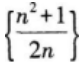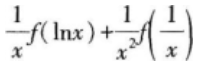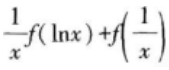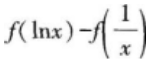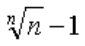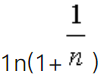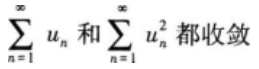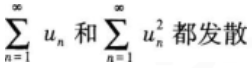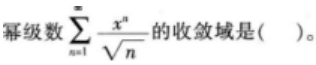

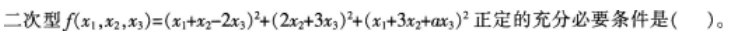
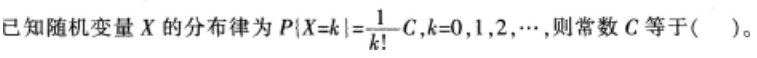

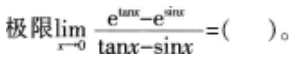
下列说法正确的是()。
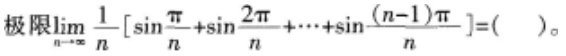
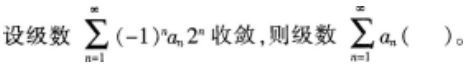
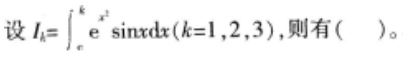



函数u=xyz-2yz-3在点(1,1,1)沿ι=2j+2j+k的方向导数为()。
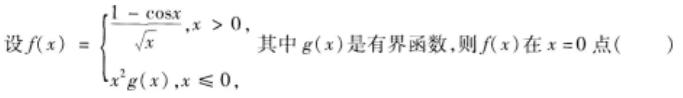


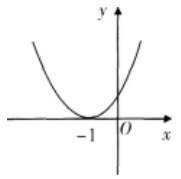
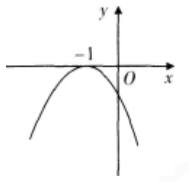
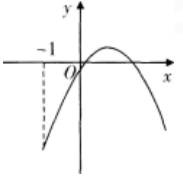
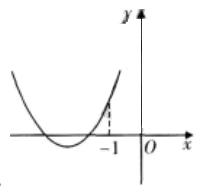
设函数ƒ(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数ƒ(x)ex的一个极值点,则下列图像不可能为ƒ(x)的图象的是( )
极限
的值是( )。
设随机变量X的分布律为
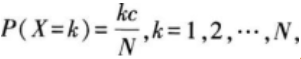
则c=( )。
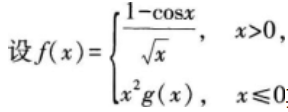
其中g(x)是有界函数,则f(x)在x=0点( )。
设函数
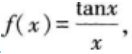
则x=0是f(x)的( )。
设函数f(x)满足
则( )。
下列数列收敛的是( )。
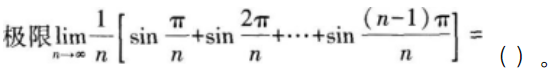
设f(x)为连续函数,且
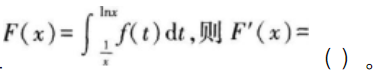
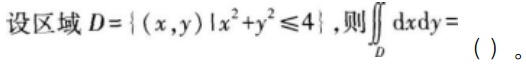
常数a>0,则级数
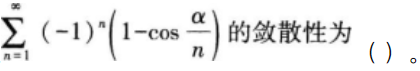
设f(x)在x=0的某邻域内存在二阶导数,

为( )。
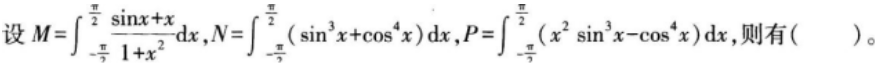
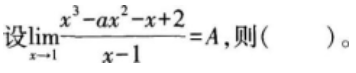

设λ=2是非奇异矩阵A的一个特征值,则矩阵
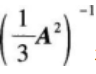
有特征值( )。
当n→∞时,下列无穷小阶数最高的是( )。
设随机变量ξ服从标准正态分布N(0,1),下列命题正确的是( )。
(1)P(|ξ|<a)=P(|ξ|<a)+P(|ξ|=a)(a>0);
(2)P(|ξ|<a)=2φ(a)-1(a>0);
(3)P(|ξ|<a)=1-2φ(a)(a>0);
(4)P(|ξ|<a)=1-P(|ξ|>a)(a>0)。
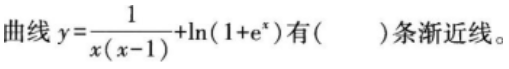
设函数f(x)在x=0处连续,
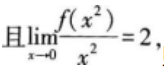
则( )。
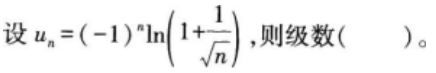
下列命题正确的个数是( )。
(1)若f(x)是[a,b]上的连续函数,则f(x)在[a,b]上可导;
(2)若函数f(x)在[a,b]上可导,则f(x)是[a,b]上的连续函数;
(3)“函数f(x)在[a,b]上可导”是“函数f(x)在[a,b]上可微”的充要条件;
(4)若f(x)是(a,b)上的连续函数,则f(x)在(a,b)上可积;
(5)若函数f(x)在[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
极限
设随机变量X的密度函数为
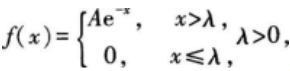
则概率P{λ<X<λ+α}(a>0)的值( )。
根据题意完成问题。
已知函数ƒ(x)=x-alnx(a∈R)。
当a=2时,求曲线y=ƒ(x)在点A(1,ƒ(1))处的切线方程;
求函数ƒ(x)的极值。
根据题意完成问题。
根据题意完成问题。
求常数a的值,使函数
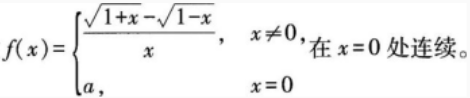
求常数a的值
设f(x)是[a,b]上的连续函数,且对于满足
的任意连续函数g(x),都有
证明存在ξ∈[a,b]使得f(x)=f(ξ)恒成立。
证明存在ξ∈[a,b]使得f(x)=f(ξ)恒成立。
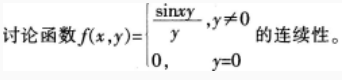
根据题意完成问题。
设f(x),g(x)在[0,1]上的导数连续,且ƒ(0)=0,ƒ´(x)≥0,g´(x)≥0。 证明:对任何a∈[0,1],有
根据题意完成问题。

根据题意完成问题。
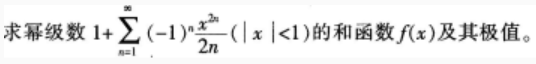
根据题意完成问题。

根据题意完成问题。
定义:一般地,对于定义在区间D上的函数y=f(x) ,①若存在x0∈D,使得f(x0)=x0, 则称x0是函数y=f(x)的一阶不动点,简称不动点;②若存在x0∈D,使f(f(x0))=x0,则称x0是函数y=f(x)的二阶不动点,简称稳定点。
若M={x|f(x)=x,x∈R} ,N={x|f(f(x))=x,x∈R} ,求证:
f(x)单调递增时,是否有N= M?证明你的结论。
设f(x),g(x)在[a,b]上连续且g(x)不变号,证明至少存在一点ξ∈[a,b],使
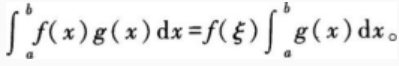
根据题意完成问题。
设随机变量X在区间(0,1)服从均匀分布,求Y=eX的概率密度。
求Y=eX的概率密度。