曲线x=t，y=t2，z=t3在点(1，1，1)处的法平面方程是()。
x+2y+3x-6=0
x+y+z-3=0
关于二次曲面x2+y2=z2，下列说法正确的是()。
已知曲面方程为x2+y2+z2-2x+8y+6z=10，则过点(5，-2，1)的切平面方程为( )。
设曲线的极坐标方程为ρ=eaθ(a>0)，则该曲线上相应于θ从0变到2π的一段弧与极轴所围成图形的面积为（ ）
已知a=(1，2，1)，b=(2，-1，1)，则过点M0(1，1，1)且同时平行于向量a和b的平面方程为（ ）
设有R2×2的子空间W={|A|A∈R2×2，AT=-A}，则W的维数是（ ）。
曲线
和两坐标轴所围成的面积是（ ）。
曲线x=t，y=t2，z=t3在点(1，1，1)处的法平面方程是（ ）。
x+2y+3z-6=0
x+y+z-3=0
设有直线
将yOz平面上的曲线z=ey(y>0)绕z轴旋转一周，所得旋转曲面方程是（ ）。
已知曲面方程为x2+y2+z2-2x+8y+6z=10，则过点(5，-2，1)的切平面方程为（ ）。
平面x-y+2z=8与平面2x+y+z=10的夹角是（ ）。
与x轴围成的平面图形绕x轴旋转一周而成的旋转体体积为（ ）。
4/3
曲线y=x(x-1)(2-x)与x轴所围成的平面图形的面积可表示为（ ）。
求由两个圆柱面x2+y2=a2与z2+x2=a2所围成立体的体积。
求由两个圆柱面x2+y2=a2与z2+x2=a2所围成立体的体积。
根据题意完成问题。
行的平面方程。
根据题意完成问题。
求实数a，b的值；
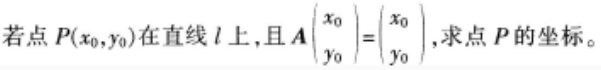
根据题意完成问题。
在空间直角坐标系中，点A，B，C的坐标依次为(-2，l，4)，(-2，2，6)，(-1，3，3)。
求三角形ABC的面积；
求四面体O-ABC的体积。
求与平面x-4z=3和2x-y-5z=1的交线平行且过点(-3，2，5)的直线的方程。
求与平面x-4z=3和2x-y-5z=1的交线平行且过点(-3，2，5)的直线的方程。
在哪个点处的切平面平行于平面2x+2y-z=0，并写出此曲面过该点的法线方程。
根据题意完成问题。
根据k的不同取值，说明(9-k)x2+(4-k)y2(1-k)z2=1表示的各是什么图形。
根据k的不同取值，说明(9-k)x2+(4-k)y2(1-k)z2=1表示的各是什么图形。
设有直线t1和t2的方程分别为
证明t1与t2异面；
求两直线之间的距离；
求与两直线距离相等的平面方程；
求与两直线都垂直相交的直线方程。
案例： 在求解题目“已知双曲线的右准线为x=4，右焦点F(10，0)，离心率e=2，求双曲线方程。”两位同学解题方法如下：
指出学生的错误之处；
分析学生的错误原因；
写出正确解法。
案例： 某教师在进行圆锥曲线的教学时．给学生出了如下一道练习题： 求过点(0，1)的直线，使它与抛物线y2=2x仅有一个公共点。 某学生的解答过程如下：
指出该生解题过程中的错误，分析其错误原因；
给出你的正确解答；
指出你解题所运用的数学思想方法。
案例： 在求解题目“已知双曲线的右准线为x=4，右焦点F(10，0)，离心率e=2，求双曲线的方程”时，两位同学解题方法如下。
指出学生的错误之处；
分析学生的错误原因；
写出正确解法。
案例：下面是高中“直线与圆的位置关系”一节的部分教材内容。
阅读这段教材，概括与圆相关的知识点；
阅读这段教材中的思考，说明设置此栏目内容的主要意图；
请说明圆与方程这一章内容在高中数学课程中的地位和作用。
