结合教学实际说一说,你认为新课程标准对教师的课堂教学有哪些要求?
结合教学实际说一说,你认为新课程标准对教师的课堂教学有哪些要求?
案例: 下面是学生小王在解答一道题目时的解法: 题目:(判断下述命题是否正确,如果正确,证明之,如果不正确,请说明理由。)
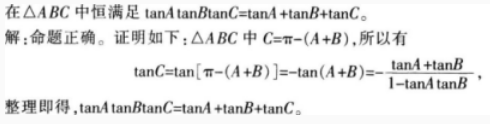
请指出学生小王的错误,并分析出现错误的原因;
如果你是小王的老师,在教学过程中如何帮助小王避免这样的错误再出现。
案例: 下面是学生小李在解答一道题目时的解法:

请指出学生小李的错误,并分析出现错误的原因;
如果你是小李的老师,在教学过程如何帮助小李避免这样的错误再出现。
案例:
面对课堂上出现的各种各样的意外生成,教师如何正确应对,如何让这些生成为我们高效的课堂教学服务,如何把自己课前的预设和课堂上的生成有效融合,从而实现教学效果的最大化,这是教师时刻面临的问题。
在一次听课中有下面的一个教学片段:教师在介绍完中位线的概念后.布置了一个操作探究活动。
师:大家把手中的三角形纸片沿其一条中位线剪开,并用剪得的纸片拼出一个四边形,由这个活动你可以得到哪些和中位线有关的结论?学生正准备动手操作,一名学生举起了手。
生:我不剪彩纸也知道结论。
师:你知道什么结论?
生:三角形的中位线平行于第三边并等于第三边的一半。
教师没有想到会出现这么个“程咬金”。脸冷了下来:“你怎么知道的?”
生:我昨天预习了,书上这么说的。
师:就你聪明,坐下!
后面的教学是在沉闷的气氛中进行的,学生操作完成后再也不敢举手发言了。
结合上面这位教师的教学过程,简要做出评析;
结合你的教学经历,说明如何处理好课堂上的意外生成。
案例:
概念同化指从已有概念出发,理解并接纳新概念的过程,实质是利用演绎方式理解和掌握概念。由于数学中大多数概念是以属概念加种差的方式定义的,所以适宜采用概念同化的方式进行教学。
以“奇函数”概念教学为例简要说明概念同化的教学模式:
(1)向学生提供“奇函数”概念的定义
(2)解释定义中的词语、符号、式子所代表的含义
突出概念刻画的是:对定义域中的任意一个自变量x,考察x与-x对应的函数值ƒ(x)与ƒ(-x)之间的关系ƒ(-x)=-ƒ(x)。因此函数的定义域应该关于原点对称,满足这个条件后再考察ƒ(-x)=-ƒ(x)。
(3)辨别例证,深化概念
教师向学生提供丰富的概念例证,例证中以正例为主,但也要包含适当的反例,尤其是一些需要考察隐含条件的例子。
(4)概念的运用
提供各种形式来运用概念,达到强化对概念的理解,促进概念体系的建构的目的,可以利用个别有一定综合性但难度不大的问题。
请举出反例说明(3)辨别例证,深化概念;
请举例补充(4)概念的运用;
请结合案例,总结出概念同化的教学模式的过程。
阅读下列两位教师的教学过程。 教师甲的教学过程: 师:在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条1000米长的线路,如何迅速查出故障所在? 如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次10米长的电线杆子,大约有200多根电线杆子呢。想一想,维修线路的工人师傅怎样工作最合理? 生1:直接一个个电线杆去寻找。 生2:先找中点,缩小范围,再找剩下来一半的中点。 师:生2的方法是不是对呢?我们一起来考虑一下。

如图,维修工人首先从中点C查,用随身带的话机向两个端点测试时,发现AC段正常,断定故障在BC段,再到BC段中点D来查,这次发现BD段正常,可见故障在CD段,再到CD中点E来查。每查一次,可以把待查的线路长度缩减一半,如此查下去,不用几次,就能把故障点锁定在一两根电线杆附近。 师:我们可以用一个动态过程来展示一下(展示多媒体课件)。 在一条线段上找某个特定点,可以通过取中点的方法逐步缩小特定点所在的范围(即二分法思想)。 教师乙的教学过程: 师:大家都看过李咏主持的《幸运52》吧,今天咱也试一回(出示游戏:看商品猜价格)。 生:积极参与游戏,课堂气氛活跃。 师:竞猜中,“高了”“低了”的含义是什么?如何确定价格最可能的范围? 生:主持人“高了、低了”的回答是判断价格所在区间的依据。 师:如何才能更快地猜中商品的预定价格? 生:回答各异。 老师由此引导学生说出“二分法”的思想,并向同学们引出二分法的概念。
分析两种情境引入的特点;
结合案例,说明为什么要学习用二分法求方程的近似解。
阅读下面有关“△ABC的三个顶点的坐标分别是A(5,1),B(7,-3),C(2,-8),求它的外接圆的方程”的三种解法,并回答问题。 解法一:设所求外接圆的方程是(x-a)2+(y-b)2=r2,A,B,C三点坐标均满足圆的方程,于是建立三元二次方程组,即
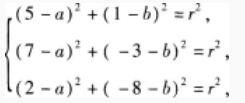
通过解方程,求出外接圆方程。 解法二:利用圆心到三个顶点的距离相等的几何性质,列出二元二次方程组,进而化简为二元一次方程,求出圆心坐标,得到外接圆方程。 解法三:利用△ABC的中垂线联立二元一次方程,求出外接圆的圆心坐标,求出方程。
分析三种解法的各自特点;
结合此案例,以优化课堂教学环节为出发点,谈谈如何处理好初高中数学教学的衔接工作。
案例: 下面是一次考试中小明同学所做的一道题的解析过程,请据此回答问题。
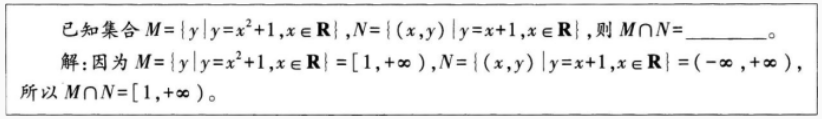
判断小明的答案是否正确,为什么?
试分析小明为什么会出现这样的错误;
教师应该如何讲解来避免这样的错误。
案例:

请指出学生小李的错误,并分析出现错误的原因;
如果你是小李的老师,在教学过程中如何帮助小李避免这样的错误再出现。


