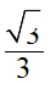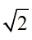极限
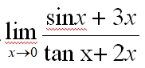
的值是( )
设α为向量m=(2,2,1)和n=(-1,2,2)的夹角,则cosα是( )
设f(x)=1/x,x∈(0,1],则下列不正确的是( )
空间曲面x2-4y2+z2=25被平面x=-3截得的曲线是( )。
甲乙两位棋手通过五局三胜制比赛争夺 1000员奖金,前三局比赛结果为甲二胜一负,现因故停止比赛,设在每局比赛中,甲乙获胜的概率都是1/2,如果按照甲乙最终获胜的概率大小分配奖金,甲应得奖金为()
已知球面方程为切线与球面相切与点 M ,线段 PM 长为
,则在点 P 的坐标中(0,0,2), z 的值为( )
计算行列式
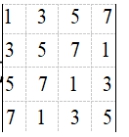
根据题意回答问题。
f(x)在[a,b]上连续,证明
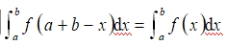
根据题意回答问题。
设A 是3*4矩阵,其秩为 3,已知n1 、n2 为非齐次线性方程组 AX=b 两个不同的解,其中
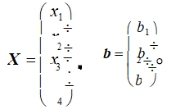
请用 n1 、n2 构造AX=0的一个解,并写出 AX=0的通解;
求 AX=b 的通解。
简述进行单元教学设计的基本流程。
根据题意回答问题。
简述数学运算的基本内涵。
根据题意回答问题。
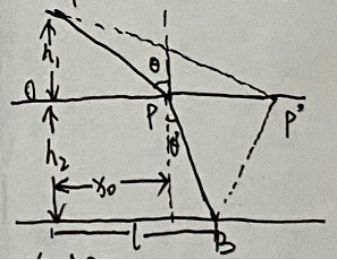
已知一束光线在空气中从点 A 到达水面上的点 P ,然后折射成水下的点 B (如图所示),射光在空气中的速度为 c ,在水中的速度为c',光线在点 P 的入射角为θ,折射角为θ'。
若OP长为x0,请写出光线从点 A 到达点 B 所需时间的表达式T(x0)
若T(x0)是光线由点 A 到达点 B 所需时间的极小值,证明sinθ/sinθ'=c/c'。
伴随着大数据时代的到来,数据分析已经深入到现代社会生活的各个方面,结合实例阐述在中学数学中培养学生数据分析能力的意义。
根据题意回答问题。
案例:“三角形中位线定理”是八年级学生的学习内容, 下面是两位教师的教学片段:
(一)教师甲
在讲授中位线定理这一内容时,利用“数学软件A ”作了两次测量,一次是验证三角形中位线定理,另一次是验证顺次连接四边形的中点所围成的图形为平行四边形。教师甲发现,当他让学生动手测量的时候,有一部分学生懒散地坐着,没有刚开始接触该软件时那样积极,课后教师向几位同学询问情况,有学生说这两道题书上都有结论,早就看过了,再去测量是不是有点儿傻?
(2)教师乙
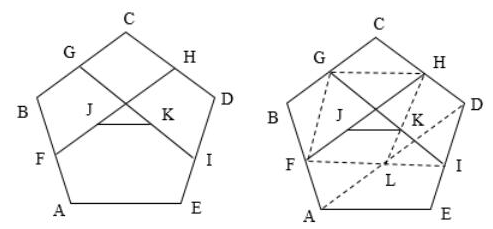
教师首先让学生探究问题,如图 2,五边形 ABCDE 中,点F、G、H、I分别是 AB、BC、CD、DE的中点, J、K分别是FH、JI的中点, AE 与 JK 有什么关系?
学生们马上打开“数学软件 A ”进行测量,很快发现 AE=4JK能不能证明发现的结论呢?学生们没有一点头绪。
教师提示说当遇到问题解决不了的时候,我们是不是进一步先解决容易的问题?教师引导学生去研究三角形中位线定理和顺次连接四边形中点所围成的图形是平行四边形两个问题,经过师生的共同研究,取 AD 的中点C 后,学生不仅验证了 AE=4JK,而且高兴地发现 AE 和JK 还存在平行关系,如图。
请分别对教师甲和乙的教学进行评价;
请画出适用于本节课教学的“三角形中位线定理”证明的示意图(图中辅助线用虚线表示);
结合本案例,请谈谈信息技术在数学中的作用。
针对“分式的基本性质”一课完成下列教学设计。
写出教学重点;
设计新知识(性质均分)的导入和探索过程;
设计一个运用分数基本性质的问题,并给出解答。