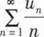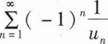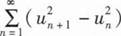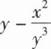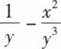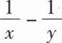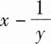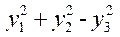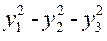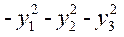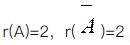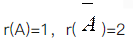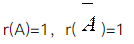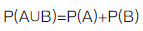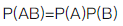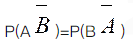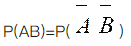当x→0时,x-tanx与xk是同阶无穷小,则k=( ).
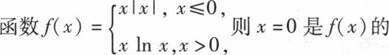
设{un}是单调增加的有界数列,则下列级数中收敛的是( ).
,如果对上半平面(y>O)内的任意有向光滑封闭曲线C都有

Q(x,y)dy=0,那么函数P(x,y)可取为( ).
设A是三阶实对称矩阵,E是三阶单位矩阵,若A2+A=2E,且|A|=4,则二次型xTAx的规范形为( ).
如图所示,有3张平面两两相交,交线相互平行,它们的方程ai1x+ai2y+ai3z=di(i=1,2,3)组成的线性方程组的系数矩阵和增广矩阵分别记为A,
,则( ).
设A,B为随机事件,则P(A)=P(B)的充分必要条件是( ).
设随机变量X和Y相互独立,且都服从正态分布N(μ,σ2),则P{|X-Y|<1}( ).
设函数f(u)可导,z=f(siny-sinx)+xy,则
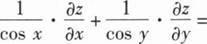
根据题意回答问题。
微分方程2yy’-y2-2=0满足条件y(0)=1的特解为______.
根据题意回答问题。
幂级数
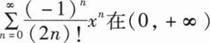
内的和函数S(x)=______.
根据题意回答问题。
设∑为曲面x2+y2+4z2=4(z≥0)的上侧,则
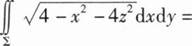
根据题意回答问题。
设A=α1,α2,α3为三阶矩阵,若α1,α2线性无关,且α3=-α1+2α2,则线性方程组Ax=0的通解为_______.
根据题意回答问题。
设随机变量x的概率密度为
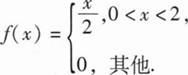
F(X)为X的分布函数,E(X)为X的数 学期望,则P{F(X)>E(X)-1}=.
根据题意回答问题。
设函数y(x)是微分方程
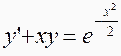
满足条件y(0)=0的特解.
求y(x);
求曲线y=y(x)的凹凸区间及拐点.
设a,b为实数,函数z=2+ax2+by2在点(3,4)处的方向导数中,沿方向l=-3i-4j的方向导数最大,最大值为10.
求a,b;
求曲面z=2+ax2+by2(z≥0)的面积.
求曲线y=e-xsinx(x≥0)与x轴之间所成图形的面积.
根据题意回答问题。
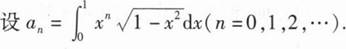
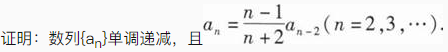
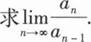
设Ω是由锥面x2+(y-z)2=(1-z)2(0≤z≤1)与平面z=0围成的锥体,求Ω的形心坐标.
根据题意回答问题。
设向量组α1=(1,2,1)T,α2=(1,3,2)T,α3=(1,a,3)T为R3的一个基,β=(1,1,1)T,在这组基下的坐标为(b,c,1)T.
求a,b,c;
证明α2,α3,β为R3的一个基,并求α2,α3,β到α1,α2,α3的过渡矩阵.
已知矩阵
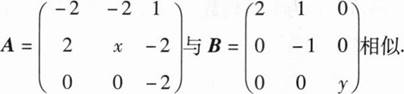
求x,y;
求可逆矩阵P,使得P-1AP=B.
设随机变量X与Y相互独立,X服从参数为1的指数分布,Y的概率分布为P{Y=-1}=p,P{Y=1}=1-p,(0<p<1),令Z=XY.
求Z的概率密度;
p为何值时,X与Z不相关?
X与Z是否相互独立?
设总体x的概率密度为
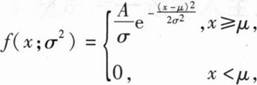
其中μ是已知参数,σ>0是未知参 数,A是常数,X1,X2,…,Xn是来自总体X的简单随机样本.
求A;
求σ2的最大似然估计量.