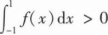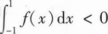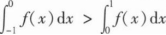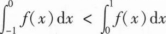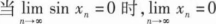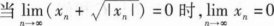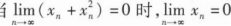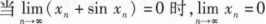若函数
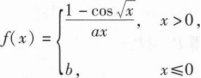
在x=0处连续,则().
设二阶可导函数f(x)满足f(1)=f(-1)=1,f(0)=-1,且f”(x)>0,则().
设数列{xn}收敛,则().
微分方程y”-4y '+8y=e2x(1+cos2x)的特解可设为y*=().
设f(x,y)具有一阶偏导数,且对任意的(x,y),都有
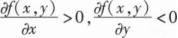
,则().
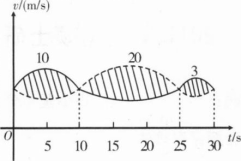
甲、乙两人赛跑,计时开始时,甲在乙前方10(单位:m)处.图中,实线表示甲的速度曲线v=v1(t)(单位:m/s),虚线表示乙的速度曲线v=v2(t),三块阴影部分面积的数值依次为10,20,3.计时开始后乙追上甲的时刻记为t0(单位:S),则().
设A为三阶矩阵,P=(α1,α2,α3)为可逆矩阵,使得
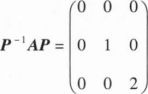
,则A(α1+α2+α3)=().
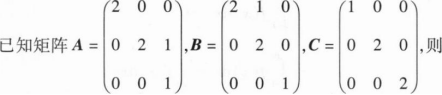
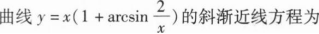
根据题意回答问题。

根据题意回答问题。
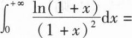
根据题意回答问题。
设函数f(x,y)具有一阶连续偏导数,且df(x,y)=yeydx+x(1+y)eydy,f(0,0)=0,则f(x,y)=_______.
根据题意回答问题。
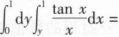
根据题意回答问题。

根据题意回答问题。

根据题意回答问题。
设函数f(u,v)具有2阶连续偏导数,y=f(ex,cos x),求
,
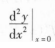
。
根据题意回答问题。
根据题意回答问题。
已知函数y(x)由方程x3+y3—3x+3y-2=0所确定,求y(x)的极值.
根据题意回答问题。
设函数f(x)在区间[0,1]上具有二阶导数,且f(1)>0,
证明:
方程f(x)=0在区间(0,1)内至少存在一个实根;
方程f(x)f”(x)+[f’(x)]2=0在区间(0,1)内至少存在两个不同的实根.
已知平面区域D={(x,y)|x2+y2≤2y},计算二重积分
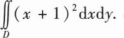
根据题意回答问题。
设y(x)是区间(0,3/2)内的可导函数,且y(1)=0,点P是曲线L:y=y(x)上的任意一点,L 在点P处的切线与Y轴相交于点(0,Yp),法线与x轴相交于点(XP,0).若XP=YP,求L上点的坐标(x,y)满足的方程.
根据题意回答问题。
设三阶矩阵A=(α1,α2,α3)有3个不同的特征值,且α3=α1+2α2.
证明:r(A)=2;
若β=α1+α2+α3,求方程组Ax=β的通解.
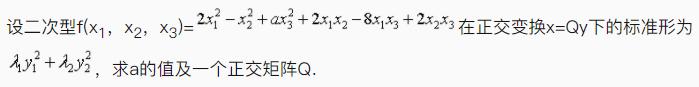
根据题意回答问题。