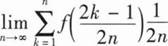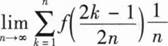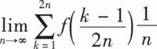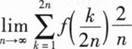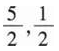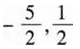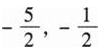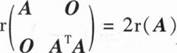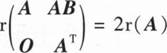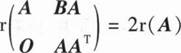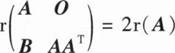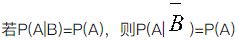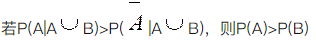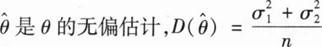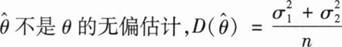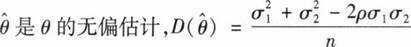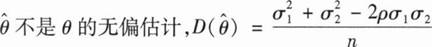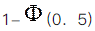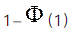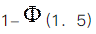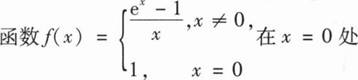
设函数f(x,y)可微,且f(x+1,ex)=x(x+1)2,f(x,x2)=2x2lnx,则df(1,1)=( ).
设函数
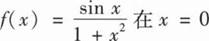
处的3次泰勒多项式为ax+bx2+cx3,则( ).
设函数f(x)在区间[0,1]上连续,则
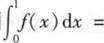
二次型f(x1,x2,x3)=(x1+x2)2+(x2+x3)2-(x3-x1)2的正惯性指数与负惯性指数依次为( ).

β2,β3两两相交,则l1,l2依次为().
设A,B为n阶实矩阵,下列结论不成立的是( ).
设A,B为随机事件,且0<P(B)<1,则下列命题中为假命题的是( ).
设(X1,Y1),(X2,Y2),…,(Xn,Yn)为来自总体
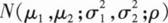
的简单随机样本,令θ=
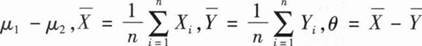
,则
设X1,X2,…,X16是来自总体N(μ,4)的简单随机样本,考虑假设检验问题:H0:μ≤10,H1:μ>10.φ(x)表示标准正态分布函数.若该检验问题的拒绝域为
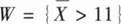
,其中
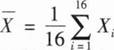
,则μ=11.5时,该检验犯第二类错误的概率为( ).
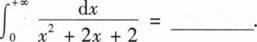
根据题意回答问题。
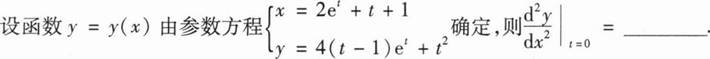
根据题意回答问题。
欧拉方程x2y”+xy’-4y=0满足条件y(1)=1,y’(1)=2的解为______.
根据题意回答问题。
设三为空间区域{(x,y,z)|x2+4y2≤4,0≤z≤2}表面的外侧,则曲面积分

y2dzdx+zdxdy=______.
根据题意回答问题。
设A=(aij)为三阶矩阵,Aij为元素aij的代数余子式.若A的每行元素之和均为2,且|A|=3,则A11+A21+A31=______.
根据题意回答问题。
甲、乙两个盒子中各装有2个红球和2个白球,先从甲盒中任取一球,观察颜色后放入乙盒中,再从乙盒中任取一球.令X,Y分别表示从甲盒和从乙盒中取到的红球个数,则X与Y的相关系数为______.
根据题意回答问题。
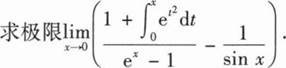
根据题意回答问题。
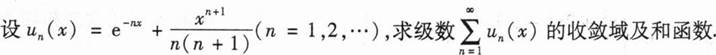
根据题意回答问题。
已知曲线
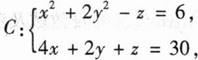
求C上的点到xOy坐标平面距离的最大值.
根据题意回答问题。

求I(D1)的值;
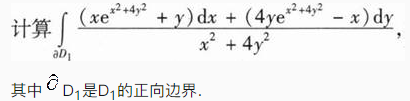
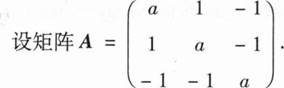
求正交矩阵P,使PTAP为对角矩阵;
求正定矩阵C,使C2=(a+3)E-A,其中E为三阶单位矩阵.
在区间(0,2)上随机取一点,将该区间分成两段,其中较短一段的长度记为X,较长一段的长度记为Y,Z=Y/X.
求X的概率密度;
求Z的概率密度;
求E(X/Y).