则事件A和事件B同时都不发生的概率是( )
求曲线y=㏑2x,直线x=1与x=5及x轴所围成平面区域的面积。
根据题意回答问题。
已知动点P与定点A (0,1,1) 的距离等于P到平面z=4距离的一半。
求动点P的轨迹方程。
动点P的轨迹方程所表示的几何图形是什么?
不透明的袋子中有10个完全相同的乒兵球,分别标有数字1到10,从袋中随机摸出1个球,记录标号后放回袋子,再随机摸出1个球,记录标号后也放回袋中。
求两次摸球的标号之和是3的概率;
求两次摸球的标号之和最大是7的概率。
列举义务教育阶段一元二次方程的三种主要解法.
根据题意回答问题。
简述义务教育阶段统计内容中数据分析的主要过程,给出描述数据集中趋势和离散程度 的统计量(各写出2个)。
根据题意回答问题。
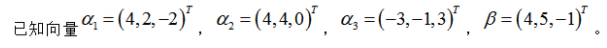
证明向量组α1,α2,α3线性无关。
将向量β用α1,α2,α3线性表示。
(1) 写出义务教务阶段涉及的不等式的性质(2条即可)
(2) 阐述不等式的性质与解一元一次不等式的关系,并举例说明
根据题意回答问题。
在某习题课上,老师让学生独立完成如下例题:
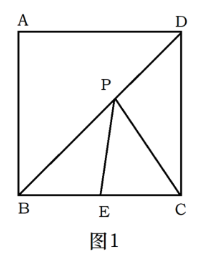
如图1,在边长为3的正方形ABCD中,E是BC中点,P是对角线BD上的动点,连接PE, PC, 当BP为何值时,PE+PC的值最小?最小值是多少?大多数学生表示不会做。 教师这样启发: 我们回顾以前学过的“饮马问题”:如图2,牧马人从A地出发,到一条笔直的河边饮马,然后回到B地,牧马人到河边什么地方饮马,所走的路径最短?
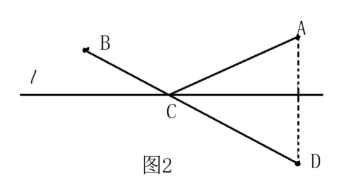
作点A关于直线的对称点D,连接BD交直线1于点C。由于AC+BC=BC+CD=BD,利用两点之间 线段最短,此时点C使AC+BC最小,点c的位置即为所求。 学生:哦,会做了……
给出该例题的求解过程。
指出该教师对学生的启发有哪些合理和不足之处。
下面是某教材有理数”一章中“绝对值”一节的内容片段: 两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处 。它们的行驶路线相同吗?它们的行驶路程相等吗?
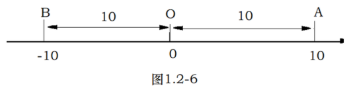
一般地, 数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|,例如,图中A, B两点分别表示10和-10,它们与原点的距离都是10个单位长度,所以10和-10的绝对值都是10, 即|10|=10,|-10|=10,显然|0|=0。 由绝对值的定义可知: 一个正数的绝对值是它本身;一个负数的绝对值是它的相反数; 0的绝对值是0。即 (1)如果a>0,那么|a|=a; (2)如果a=0,那么|a|=0; (3)如果a < 0,那么|a|=-a 根据上述内容,完成下列任务:
写出其中蕴含的主要数学思想方法;
完成“绝对值"这节课的教学设计。要求写出教学目标、教学重点和主要教学过程(含情境导入、概念理解、概念巩固)。


