曲线
的斜渐近线方程为( )

极限
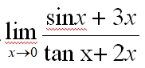
的值是( )
三个非零向量共面,则下列结论不一定成立的是( )。




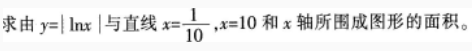
袋中有1个红球、2个黑球与3个白球,现有放回地从袋中取两次,每次取一个球,以X,Y,Z分别表示两次取球所取得的红球、黑球与白球的个数。
求P|X=1|Z=0};
求二维随机变量(X,Y)的概率分布。
数形结合思想是一种重要的数学思想,它的实质就是根据数与形之间的对应关系,通过数与形的相互转化来解决问题。用数形结合思想解题能简化推理和运算,具有直观、快捷的优点。
请简要谈谈数形结合思想在解哪些类型的问题时可以发挥作用,使问题得到更好的解决。
“巩固与发展相结合”是数学教学的基本原则。谈谈“巩固”与“发展”的关系,教师在教学过程中怎样做到在发展的过程中进行巩固。
“巩固与发展相结合”是数学教学的基本原则。谈谈“巩固”与“发展”的关系,教师在教学过程中怎样做到在发展的过程中进行巩固。
下面是“同底数幂的乘法”的教学片段:师生共同探索归纳总结出同底数幂的乘法法则后,进入知识巩固环节,教师出示例题:已知2x=16,2y=512,求2x+y的值。
解决本题时,需要学生能理解同底数幂的乘法法则,将公式am·an=an+m逆用,由于题目本身相对简单,因此大多数学生能获得解题思路并求得结果。(注:学生的回答是2x+y=2x.2y=16X512=8192)
一位学生出现了不同的声音,他的思路,先设法求x,y的值,然后代入求2x+y,的值。
教师点评:“你这样做也对,但若已知2y=514,你有本事求得到y的值吗?如果2y=456312.你还敢求出y的值吗?”
分析上述教学片段,指出教学过程中师生教学行为的可取之处;
对教学过程中存在的问题进行原因分析并给出教学对策。
设顾客在某银行窗口等待服务的时间X(min)的概率密度为
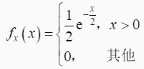
用变量Y表示顾客对银行服务质量的评价值若顾客等待时间不超过5(min) 则评价值为Y =1;否则,评价值为y=-1,即
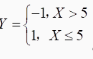
求X的分布函数。
求Y的分布律。
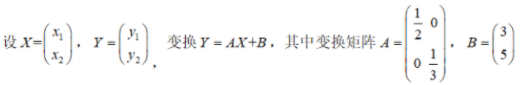

举例说明在该变换下什么性质保持不变,什么性质发生变化(例如距离、斜率等)


