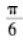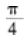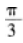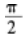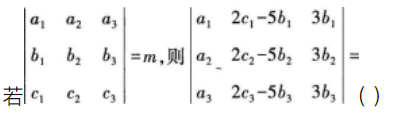
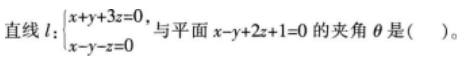
曲面z=4-x2-y2上点P处的切平面平行于平面2x+2y+z-1=0,则点P的坐标是()。
已知2n阶行列式D的某一列元素及其余子式都等于a,则D=( )
抛掷两粒正方体骰子(每个面上的点数分别为1, 2, .... 6),假定每个面朝上的可能性相同,观察向上的点数,则点数之和等于5的概率为()
已知圆C:(x-1)2+(y-2)2=25及直线l:(2m+1)x+(m+1)y=7m+4(m∈R)。
证明:不论m取什么实数,直线Z与圆C恒相交。
数学教师在对信息技术资源进行开发与利用时需要关注哪些方面?
数学教师在对信息技术资源进行开发与利用时需要关注哪些方面?
“中心对称和中心对称图形”的教学目的主要有①知道中心对称的概念,能说出中心对称的定义和关于中心对称的两个图形的性质。②会根据关于中心对称图形的性质定理2的逆定理来判定两个图形关于一点对称;会画与已知图形关于一点成中心对称的图形。此外,通过复习图形轴对称,并与中心对称比较,渗透类比的思想方法;用运动的观点观察和认识图形,渗透旋转变换的思想。
通过题干来完成下列教学设计。
给出本课程的课题引入;
根据教学目标设计教学环节;给出两个实例以进行知识探究。
数学运算能力是中学数学教学需要培养的基本能力。学生的数学运算能力具体表现为哪些方面?请以整式运算为例予以说明。
根据题意回答问题。
平方差公式a2-b2=(a+b)(a-b)是初中乘法公式的内容之一。 某教师教学时,将引导学生归纳猜想平方差公式作为教学过程的环节之一,设计思路如下: 假定b=1。问题简化为:a2-1=?

教学设计简述该教师在该环节的教学设计意图。
教学设计简述平方差公式在初中数学中的地位。
教学设计请给出平方差公式的教学目标,并设计教学流程。
教学设计请通过图示给出平方差公式的几何背景。
针对“分式的基本性质”一课完成下列教学设计。
写出教学重点;
设计新知识(性质均分)的导入和探索过程;
设计一个运用分数基本性质的问题,并给出解答。
案例:甲、乙两位数学教师均选用如下素材组织了探究活动,如图 1 所示,这是一个三级台阶,它的每一级的长、宽、高分别为50cm,25cm和15 cm,A和B是这个台阶的两个相对端点,B点上有一只蚂蚁,想到A点去吃食物。请你想一想,这只蚂蚁从B点出发,沿着台阶面爬到A点的最短路线是什么?
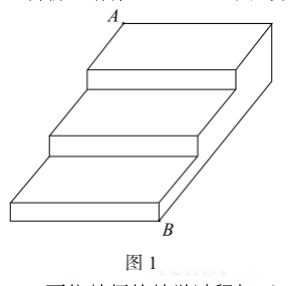
两位教师的教学过程如下: 【甲教师】 用大屏幕展示问题情境,组织小组讨论,学生开始读题,教师巡视过程中看到有的同学把台阶画出来,与教学预设不符,立即中止了大家讨论,指着题目说:“同学们请注意读题,是‘沿着台阶面’,你们把这张图画出来有什么用?” 在接下来的讨论中,教师又遇到新情况,有的学生画展开图,却把尺寸弄错了,于是教师终止思考。 【乙教师】 展示情境,将问题进行分析,出示了一张台阶模样的纸片,边说边将纸片拉直,如图 2 所示,然后让大家研究。很快,有同学说出答案,教师解释了一下,同学们都明白了。
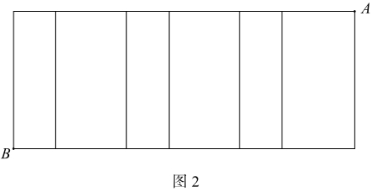
甲、乙教师课后交流:两个教师在教学中均有探究。
《义务教育数学课程标准(2011 年版)》指出,“有效的数学教学活动是教师教与学生学的统一”,教师应成为学生学习活动的组织者、引导者、合作者。请说明两位教师的教学是否符合要求;
两位教师组织的探究活动各自存在什么问题,请简要说明并简述理由;
组织数学探究活动,需要注意哪些事项?请说明。
针对“角平分线的性质定理”的内容,请你完成下列任务:
叙述角平分线的性质定理;
设计“角平分线的性质定理“教学过程(只要求写出新课导入、定理形成与证明过程),并说明设计意图;
借助“角平分线的性质定理”,简述如何帮助学生积累认识几何图形的数学活动经验.
在某习题课上,老师让学生独立完成如下例题:
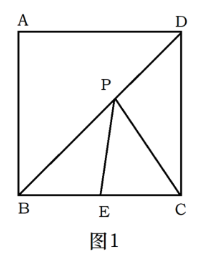
如图1,在边长为3的正方形ABCD中,E是BC中点,P是对角线BD上的动点,连接PE, PC, 当BP为何值时,PE+PC的值最小?最小值是多少?大多数学生表示不会做。 教师这样启发: 我们回顾以前学过的“饮马问题”:如图2,牧马人从A地出发,到一条笔直的河边饮马,然后回到B地,牧马人到河边什么地方饮马,所走的路径最短?
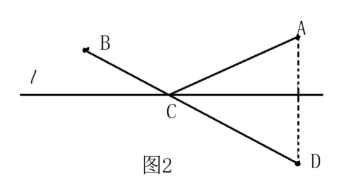
作点A关于直线的对称点D,连接BD交直线1于点C。由于AC+BC=BC+CD=BD,利用两点之间 线段最短,此时点C使AC+BC最小,点c的位置即为所求。 学生:哦,会做了……
给出该例题的求解过程。
指出该教师对学生的启发有哪些合理和不足之处。