设A是n阶矩阵,则|(2A)*|=( )
已知随机变量x与y有相同的不为0的方差,则X与Y,的相关系数ρ=1的充要条件是( )
极限
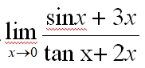
的值是( )
三个非零向量共面,则下列结论不一定成立的是( )。
已知函数f(x)=ex+2x2-3x。 (1)求曲线y=f(x)在点(1,f(1))处的切线方程;

已知函数f(x)=ex+2x2-3x。 (1)求曲线y=f(x)在点(1,f(1))处的切线方程;

如下图所示,设0<a<b,函数ƒ(x)在[a,b]上连续,在(a,b)可微且ƒ(x)>0,ƒ(a)= ƒ(b)。设ι为绕原点O可转动的细棍(射线),放手后落在函数ƒ(x)的图像上并支撑在点A(ζ,ƒ(ζ))上,从直观上看。
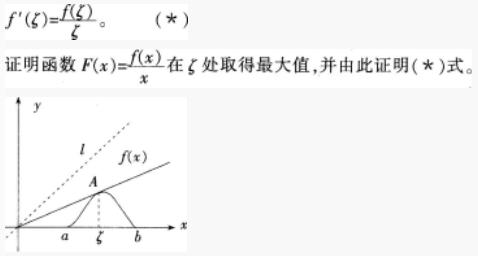
如下图所示,设0<a<b,函数ƒ(x)在[a,b]上连续,在(a,b)可微且ƒ(x)>0,ƒ(a)= ƒ(b)。设ι为绕原点O可转动的细棍(射线),放手后落在函数ƒ(x)的图像上并支撑在点A(ζ,ƒ(ζ))上,从直观上看。


用长为50厘米的细绳围成一个边长为整厘米的长方形,怎样才能使面积达到最大?以此为例,在对学生数学思考和问题解决目标进行评价时,教师可以关注以哪几个不同的层次?
用长为50厘米的细绳围成一个边长为整厘米的长方形,怎样才能使面积达到最大?以此为例,在对学生数学思考和问题解决目标进行评价时,教师可以关注以哪几个不同的层次?
“巩固与发展相结合”是数学教学的基本原则。谈谈“巩固”与“发展”的关系,教师在教学过程中怎样做到在发展的过程中进行巩固。
“巩固与发展相结合”是数学教学的基本原则。谈谈“巩固”与“发展”的关系,教师在教学过程中怎样做到在发展的过程中进行巩固。

判断学生1和学生2的解法正确吗?并说明理由。
如果你是该教师,如何完成后续的教学?
“变量与函数”是初中数学教学中的重要内容,请完成下列任务:
在“变量与函数”起始课的“教学重点”设计中,有两种方案:
①强调认识变量、常量,用式子表示变量间关系。
②强调能指出具体问题中的常量、变量。初步理解存在一类变量可以用函数方式来刻画。你赞同哪种方案?简述理由。
给出y=4x+6以及4x+6=0,则指出哪个是函数,如果是函数,它的变量是什么?常量是什么?
为了让初中生充分认识“变量与函数”中“变量”的概念,作为教师应该对此有深刻的理解,请谈谈你对“变量”概念的认识。
已知平面上一椭圆,长半轴长为a,短半轴长为b,0<b<a,求该椭圆绕着长轴旋转一周所得到的旋转体的体积。
根据题意回答问题。
简述数学运算的基本内涵。
根据题意回答问题。


