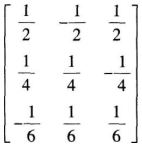
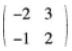已知三维向量空间的基为a1=(1,1,0),a2=(1,0,1),a3=(0,1,1),则向量β=(2,0,0)在此基底下的坐标是()。
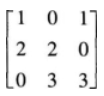
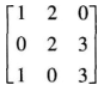
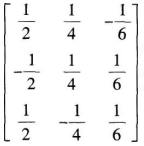
设α1,α2,α3是三维向量空间R3的一个基,则由基α1,1/2α2,1/3α3到基α1+α2,α2+α3,α3+α1的过渡矩阵为( )。
是正定二次型,则t的取值范围是( )。
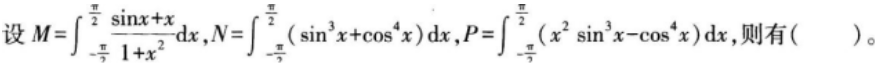
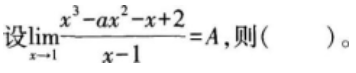
设f(x),g(x)在[0,1]上的导数连续,且ƒ(0)=0,ƒ´(x)≥0,g´(x)≥0。 证明:对任何a∈[0,1],有
根据题意完成问题。
案例: 某教师在进行圆锥曲线的教学时.给学生出了如下一道练习题: 求过点(0,1)的直线,使它与抛物线y2=2x仅有一个公共点。 某学生的解答过程如下:

指出该生解题过程中的错误,分析其错误原因;
给出你的正确解答;
指出你解题所运用的数学思想方法。
“巩固与发展相结合”是数学教学的基本原则。谈谈“巩固”与“发展”的关系,教师在教学过程中怎样做到在发展的过程中进行巩固。
“巩固与发展相结合”是数学教学的基本原则。谈谈“巩固”与“发展”的关系,教师在教学过程中怎样做到在发展的过程中进行巩固。
《普通高中数学课程标准(实验)》指出“教师教学应该以学生的认知发展水平和已有的经验为基础,面向全体学生,注重启发式和因材施教。教师要发挥主导作用,处理好讲授与学生自主学习的关系,引导学生独立思考、主动探索、合作交流.使学生理解和掌握基本的数学知识与技能、数学思想和方法,获得基本的数学活动经验。”
简要说明数学思想方法的含义,并给出高中数学教学中常用的几种数学思想方法(至少5种),且任选一种思想进行举例说明,以及如何在教学过程中让学生感悟这种思想。
结合教学实际说一说,你认为新课程标准对教师的课堂教学有哪些要求?
结合教学实际说一说,你认为新课程标准对教师的课堂教学有哪些要求?
阅读下列两位教师的教学过程。 教师甲的教学过程: 师:在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条1000米长的线路,如何迅速查出故障所在? 如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次10米长的电线杆子,大约有200多根电线杆子呢。想一想,维修线路的工人师傅怎样工作最合理? 生1:直接一个个电线杆去寻找。 生2:先找中点,缩小范围,再找剩下来一半的中点。 师:生2的方法是不是对呢?我们一起来考虑一下。

如图,维修工人首先从中点C查,用随身带的话机向两个端点测试时,发现AC段正常,断定故障在BC段,再到BC段中点D来查,这次发现BD段正常,可见故障在CD段,再到CD中点E来查。每查一次,可以把待查的线路长度缩减一半,如此查下去,不用几次,就能把故障点锁定在一两根电线杆附近。 师:我们可以用一个动态过程来展示一下(展示多媒体课件)。 在一条线段上找某个特定点,可以通过取中点的方法逐步缩小特定点所在的范围(即二分法思想)。 教师乙的教学过程: 师:大家都看过李咏主持的《幸运52》吧,今天咱也试一回(出示游戏:看商品猜价格)。 生:积极参与游戏,课堂气氛活跃。 师:竞猜中,“高了”“低了”的含义是什么?如何确定价格最可能的范围? 生:主持人“高了、低了”的回答是判断价格所在区间的依据。 师:如何才能更快地猜中商品的预定价格? 生:回答各异。 老师由此引导学生说出“二分法”的思想,并向同学们引出二分法的概念。
分析两种情境引入的特点;
结合案例,说明为什么要学习用二分法求方程的近似解。

行列式②的几何意义是什么?
上述结论的几何意义是什么?



有人认为目前的教学缺乏对中学生思维能力的培养,请谈一谈你的看法,并说一说在老师在教学中应该如何做。
根据题意回答问题。