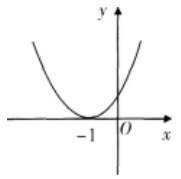
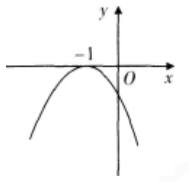
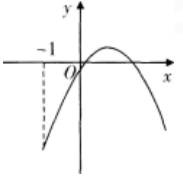
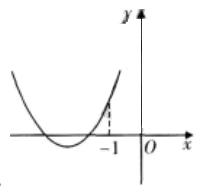
设4阶矩阵A与B仅有第3行不同,且|A|=1,|B|=2,则|A+B|=( )。
设a1=(1,2,3,1)T,a2=(3,4,7,-1)T,a3=(2,6,a,6)T,a4=(0,1,3,a)T,那么a=8是a1,a2,a3,a4线性相关的( )

设函数ƒ(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数ƒ(x)ex的一个极值点,则下列图像不可能为ƒ(x)的图象的是( )
常数a>0,则级数
某教师针对《二项式定理》设计了一节习题课,下面是两位同学所做的一道例题的解 题过程,据此回答问题。

给出案例中例题的正确解法;
请指出案例中两个学生解题中的错误,并分析产生错误的原因;
结合案例,谈谈在教学“二项式定理”内容时应该注意哪些问题。
案例: 某教师在进行圆锥曲线的教学时.给学生出了如下一道练习题: 求过点(0,1)的直线,使它与抛物线y2=2x仅有一个公共点。 某学生的解答过程如下:

指出该生解题过程中的错误,分析其错误原因;
给出你的正确解答;
指出你解题所运用的数学思想方法。
案例: 在求解题目“已知双曲线的右准线为x=4,右焦点F(10,0),离心率e=2,求双曲线的方程”时,两位同学解题方法如下。

指出学生的错误之处;
分析学生的错误原因;
写出正确解法。
某市旅游局为了了解游客情况,针对情况制定策略,在某月中随机抽取甲、乙两个景点各10天的游客数,统计得到茎叶图如下:
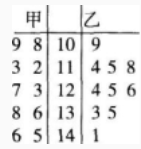
若将图中景点甲中的数据作为该景点较长一段时期内的样本数据,以每天游客人数频率为概率P。今从这段时期内任取4天,记其中游客数超过130人的天数为ξ,求P(ξ≤2);
现从上图20天的数据中任取2天(甲、乙各1天),记其中游客数不低于125且不高于135人的天数为η,求η的分布列和数学期望。
分别解释学习心理学中“同化”与“顺应”的含义,并举例说明“同化”在数学概念学习中的作用。
分别解释学习心理学中“同化”与“顺应”的含义,并举例说明“同化”在数学概念学习中的作用。
理论与实践相结合,既是认识论与方法论的基本原理,又是教学论中的一般原理。结合新课程改革,谈谈你对新课程实施过程中数学教学方法应如何进行创新的观点。
谈谈你对新课程实施过程中数学教学方法应如何进行创新的观点。
数学教学要体现课程改革的基本理念,请谈谈在教学中应该把握好哪几方面的问题。
数学教学要体现课程改革的基本理念,请谈谈在教学中应该把握好哪几方面的问题。
《普通高中数学课程标准(实验)》指出:“形式化是数学的基本特征之一。在数学教学中,学习形式化的表达是一项基本要求,但是不能只限于形式化的表述,要强调对数学本质的认识,否则会将生动活泼的数学思维活动淹没在形式化的海洋里。数学的现代发展也表明,全盘形式化是不可能的。因此,高中数学课程应该返璞归真,努力揭示数学概念、法则、结论的发展过程的本质。”
如何理解数学形式化?如何适度形式化?并举例说明几种不同的形式化数学内容的教学方式。
在学习了“直线与圆的位置关系”后,一位教师让学生解决如下问题:

指出上述解法的错误之处,分析错误原因,并给出两种正确解法。
针对该题的教学,谈谈如何设置问题,帮助学生避免出现上述错误。