极限
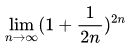
的值是( )。
设A和B为n阶方阵子一定正确的是( )。
甲、乙两位同学分别前往不同公司的面试,甲同学被选中的概率是1/7,乙同学被选中的概率是1/5,则两位同学中至少有一位被选中的概率是()。
若向量a=(1,0,1), a2=(0,1,1), a3=(2, λ,2)线性相关, 则 λ的值为()。
①2x<1
②x-3是整数
③存在一个x∈z,使2x-1=5
④对任意一个无理数x,x+2也是无理数
①勾股定理②对数③割圆术 ④更相减损术
已知函数f(x)=x4-4x3+4x2+1,求函数f(x) 的单调区间和极值。
根据题意回答问题。
求过直线
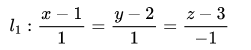
且平行于于直线
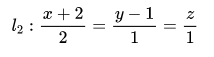
的平面方程。
根据题意回答问题。
已知某班级80%的女生和90%的男生选修滑冰,且该班中60%的学生是女生。
从该班随机选取一 名学生,求这名学生选修滑冰的概率。
在该班选修滑冰的学生中随机选取一名学生, 求这名学生是女生的概率。
简述研究椭圆几何性质的两种方法。
根据题意回答问题。
简述在教材平面教学设计内容中设置下列习题的设计意图(答出两条即可)。已知0<x<1,0<y<1,求证不等式

并说明其设计意义。
根据题意回答问题。
已知抛物线
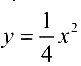
。
求抛物线在点(2,1)处的切线方程。
如图,抛物线在点P(xo, yo)(xo ≠0)处的切线PT与y轴交于点M,光源在抛物线焦点F(0,1)处,入射光线FP经抛物线反射后的光线为PQ,即∠FPM =∠QPT,求证: 直线PQ与y轴平行。

论述数学史在数学教学各阶段(导入、形成、应用)的作用。
根据题意回答问题。
下面是甲、乙两位教师的教学片段。 [教师甲] 教师甲:在平面直角坐标系中,点(x, y)关于y轴的对称点是什么? 学生1: (-x, y)。 教师甲:为了研究函数的对称性,请大家填写下表,观察给定函数的自变量x互为相相反数时,对应的函数值之间具有什么关系?
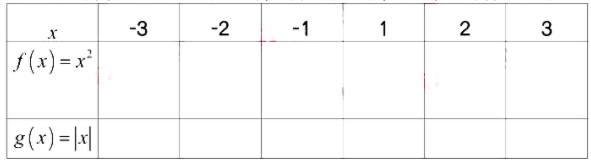
学生2:通过计算发现,自变量互为相反数时,对应的函数值相等,可以用解析表示,

教师甲:通常我们把具有以上特征的函数称为偶函数,请大家试着给出偶函数的定义。 [教师乙] 教师乙:我们已经研究了函数的单调性,并且用符号语言精确地描述了函数的单调性,今天我们研究函数的其他性质,请大家画出函数f(x)=x2和g(x)= |x|的图象,并观察它们的共同特征。 (通过观察,学生发现这函数的图象都关于y轴对称) 教师乙:类比函数的单调性,你能用符号语言精确地描述“数图象关于y轴对称”这概念吗? (通过观察,学生发现f(-x)=f(x).) 教师乙:通常我们把函数上述特征的函数称为偶函数,请大家试着给出偶函数的定义。
写出偶函数的定义,并简要说明函数奇偶性的作用。
对甲、乙两位教师的教学进行评价。
下面是高一下学期教材“空间中直线与平面的位置关系”的部分内容。

画出直线与平面的位置关系的示意图,并举出生活中体现这三种位置关系的实例。
写出这部分内容的教学设计,包括教学目标、教学重点、教学过程(含引导学生探究的活动和设计意图)。


